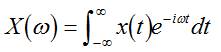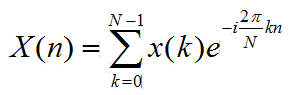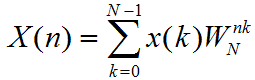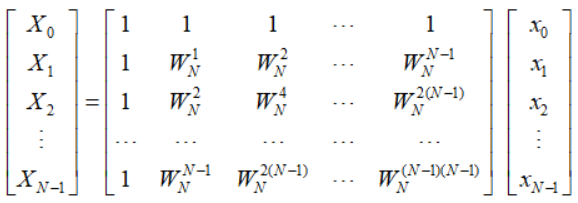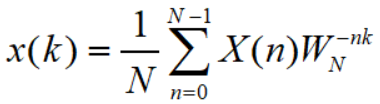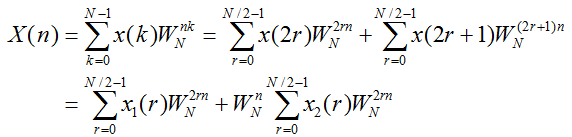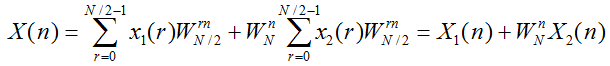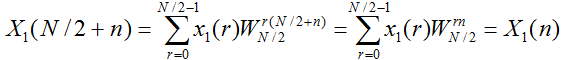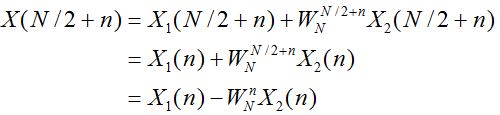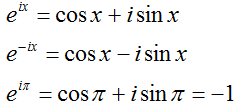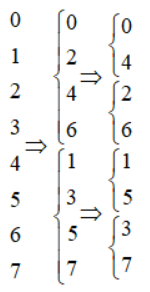快速傅里叶算法(FFT)示例

作者：追风剑情 发布于：2018-2-23 18:25 分类：Algorithms

连续非周期信号的傅里叶变换公式

111.png(公式中的i是虚数单位)

现在假设在x(t)的某一段连续区间上以周期T进行采样，得到N个采样点，则每个采样点的离散傅里叶变换公式就是：

2222.png(n=0,1,...,N-1)

令33333.png,则上式可简单记为:

44444.png(n=0,1,...,N-1)

上式可用线性方程组表示为:

111111.png 

for (int n=0; n<N; n++)
	for (int k=0; k<N; k++)
		int p = n * k;//旋转因子指数


逆变换公式

111111.png

11111.png被称为旋转因子。

77.png的周期性可以表示为5555.png

77.png的对称性可以表示为6666.png

77.png的可约性可以表示为22222.png

原始信号与两个分组信号之间的关系:

每次分解，都将原始信号x(n)按照时间顺序(也就是n的序号)分成奇、偶两个组x1(r)和x2(r)，其中r与n的关系是:

当n为偶数时，令n=2r;

当n为奇数时，令n=2r+1;

也就是说，原始信号与两个分组的信号存在以下关系:

x(2r)=x1(r), x(2r+1)=x2(r)  其中r=0,1,...,N/2-1

将一个N点DFT分解为两个N/2点DFT：

88888.png

因为9999.png，代入上式，得到：

00000.png

由周期性可知:111.png,因此：

2222.png

同理可得：3333.png

由以上关系可知：

一个N点DFT变换的前N/2个周期数据的转换关系是:

4444.png (n=0,1,...,N/2-1)

一个N点DFT变换的后N/2个周期数据的转换关系是:

5555.png(n=0,1,...,N/2-1)

2222.png

欧拉公式

3333.png

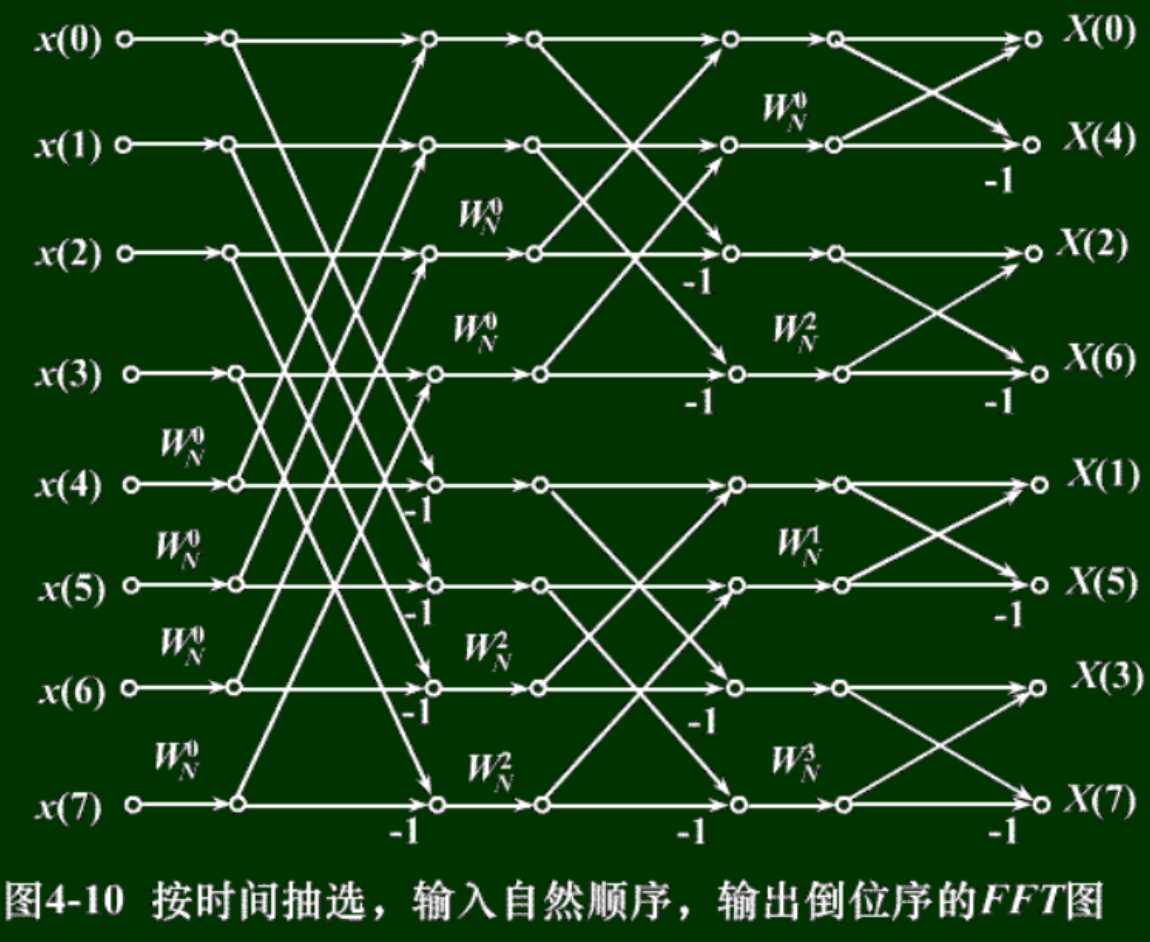
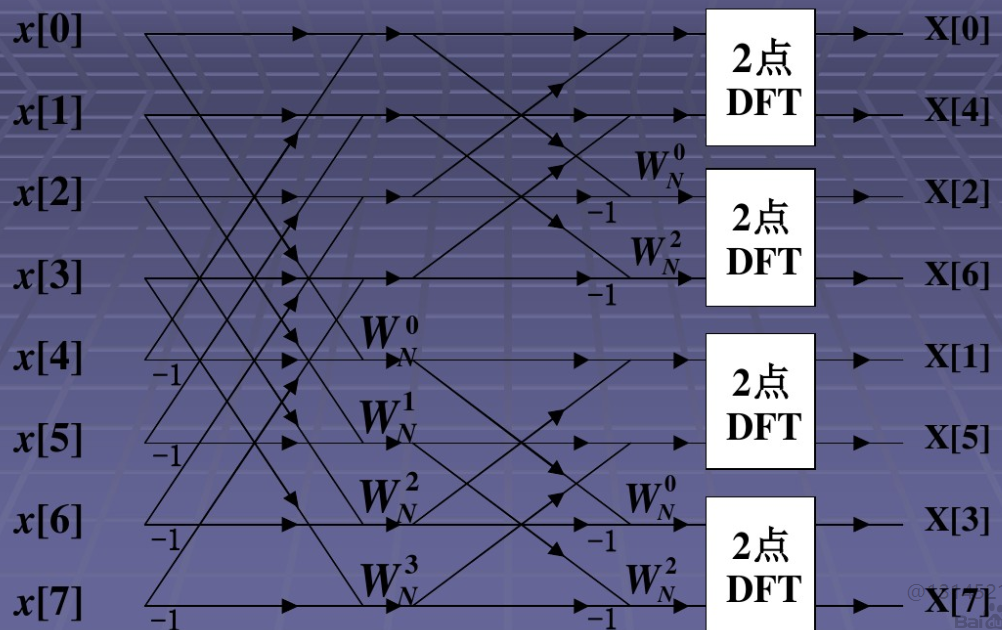
从上面的公式可知，FFT是递归求解过程。不断对数据进行奇偶分组，如下图:

11111.png

蝶形算法流程图(借用网上一张截图)

输出倒位序的FFT流程图.png

11111.png

旋转因子WNP规律
P = i*(1<<L); (i为第几次蝶形运算, L为当前级数(从0开始算))

111111.png

FFT算法的复量运算量为

111111.png

图像处理：先进行行变换，再对变换结果进行列变换，或者先进行列变换，再对结果进行行变换。

二维离散傅里叶变换
二维离散傅里叶变换(C#版)

示例 


using System;
using System.Collections.Generic;

namespace ConsoleApp34
{
    class Program
    {
        static void Main(string[] args)
        {
            TestFFT();
            TestFFT2();
            Console.Read();
        }

        private static void TestFFT()
        {
            const int N = 8;
            //初始化时域数据
            Complex[] TD2FD = new Complex[N];
            for (int i = 0; i < N; i++)
            {
                Complex cpx = new Complex();
                cpx.re = i;
                cpx.im = 0;
                TD2FD[i] = cpx;
            }
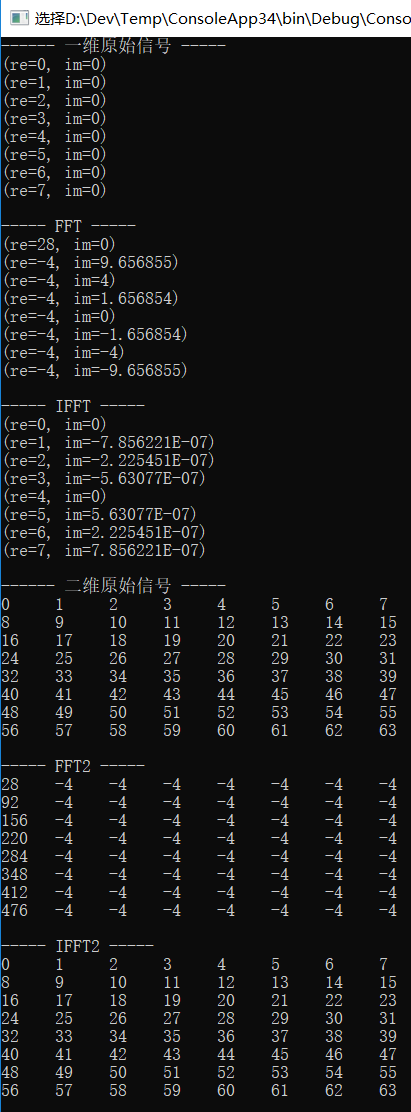
            Console.WriteLine("------ 一维原始信号 -----");
            Print(TD2FD);

            Console.WriteLine("----- FFT -----");
            FFT(TD2FD);
            Print(TD2FD);

            Console.WriteLine("----- IFFT -----");
            IFFT(TD2FD);
            Print(TD2FD);
        }

        private static void TestFFT2()
        {
            const int W = 8, H = 8;
            Complex2D complex2D = new Complex2D(W, H);
            for (int i=0; i<H; i++)
            {
                for (int j=0; j<W; j++)
                {
                    Complex cpx = new Complex();
                    cpx.re = i * W + j;
                    cpx.im = 0;
                    complex2D.SetComplex(i, j, cpx);
                }
            }

            Console.WriteLine("------ 二维原始信号 -----");
            complex2D.Print();

            Console.WriteLine("----- FFT2 -----");
            FFT2(complex2D);
            complex2D.Print();

            Console.WriteLine("----- IFFT2 -----");
            IFFT2(complex2D);
            complex2D.Print();
        }

        //快速傅里叶变换
        public static void FFT(Complex[] TD2FD)
        {
            FFT_Core(TD2FD, WT_LUT(TD2FD.Length, 1));
        }

        //快速傅里叶变换 (二维)
        public static void FFT2(Complex2D TD2FD)
        {
            //对每一行做FFT
            for (int i=0; i<TD2FD.Height; i++)
            {
                Complex[] row = TD2FD.GetRow(i);
                FFT(row);
            }

            //对每一列做FFT
            for (int i = 0; i < TD2FD.Width; i++)
            {
                Complex[] column = TD2FD.GetColumn(i);
                FFT(column);
            }
        }

        //快速傅里叶逆变换
        public static void IFFT(Complex[] FD2TD)
        {
            //做FFT变换
            Complex[] WT = WT_LUT(FD2TD.Length, -1);
            FFT_Core(FD2TD, WT);
            //除以N
            for (int i = 0; i < FD2TD.Length; i++) {
                FD2TD[i].re /= FD2TD.Length;
                FD2TD[i].im /= FD2TD.Length;
            }
        }

        //快速傅里叶逆变换 (二维)
        public static void IFFT2(Complex2D FD2TD)
        {
            //对每一行做IFFT
            for (int i = 0; i < FD2TD.Height; i++)
            {
                Complex[] row = FD2TD.GetRow(i);
                IFFT(row);
            }

            //对每一列做IFFT
            for (int i = 0; i < FD2TD.Width; i++)
            {
                Complex[] column = FD2TD.GetColumn(i);
                IFFT(column);
            }
        }

        // 返回旋转因子查询表(twiddle factor lookup table)
        private static Complex[] WT_LUT(int N, int flag = 1)
        {
            Complex[] WT = new Complex[N];
            for (int i = 0; i < N; i++)
            {
                Complex cpx_wt = new Complex();
                float angle = (float)(-i * Math.PI * 2 / N);
                cpx_wt.re = (float)Math.Cos(angle);
                //IFFT flag=-1, FFT flag=1
                cpx_wt.im = flag * (float)Math.Sin(angle);
                WT[i] = cpx_wt;
            }
            return WT;
        }

        private static void FFT_Core(Complex[] TD2FD, Complex[] WT)
        {
            int power = (int)Math.Log(TD2FD.Length, 2);
            int butterfly;
            int p, s;
            Complex x1, x2, wt;

            //倒位排序
            BitReverse(TD2FD);

            //蝶形运算
            for (int k = 0; k < power; k++) //级数
            {
                for (int j = 0; j < 1 << (power - k - 1); j++) //组数
                {
                    //每组有几个元素
                    butterfly = 1 << k + 1;
                    //计算参与蝶形运算的两个元素的索引
                    p = j * butterfly;
                    s = p + butterfly / 2;
                    for (int i = 0; i < butterfly / 2; i++) //蝶形运算次数
                    {
                        x1 = TD2FD[i + p];
                        x2 = TD2FD[i + s];
                        wt = WT[i * TD2FD.Length / butterfly];
                        TD2FD[i + p] = x1 + x2 * wt;
                        TD2FD[i + s] = x1 - x2 * wt;
                    }
                }
            }
        }

        private static int BitReverse(int x)
        {
            //倒位排序
            //0   1   2   3   4   5   6   7   十进制
            //000 001 010 011 100 101 110 111 十进制对应的二进制
            //000 100 010 110 001 101 011 111 码位反转
            //0   4   2   6   1   5   3   7   码位反转后对应的十进制
            int[] table = new int[8] { 0, 4, 2, 6, 1, 5, 3, 7 };
            return table[x];
        }

        // 倒位排序——雷德算法
        private static void BitReverse(Complex[] array)
        {
            int i, j, k;
            int N = array.Length;
            Complex temp;
            j = 0;

            for (i = 0; i < N - 1; i++)
            {
                if (i < j)
                {
                    temp = array[i];
                    array[i] = array[j];
                    array[j] = temp;
                }
                // 求j的下一个倒序位
                // N/2的二进制最高位为1，其他位都为0
                // 判断最高位是否为1，可与N/2进行比较
                // 判断次高位是否为1，可与N/4进行比较
                k = N >> 1;
                //如果k<=j,表示j的最高位为1
                while (k <= j)
                {
                    //当k<=j时，需要将最高位变为0
                    j = j - k;
                    //判断次高位是否为1,依次类推，逐个比较，直到j某个位为0
                    k >>= 1;
                }
                j = j + k;//将0变为1
            }
        }

        // 打印
        private static void Print(Complex[] TD2FD)
        {
            for (int i = 0; i < TD2FD.Length; i++)
            {
                Console.WriteLine("(re={0}, im={1})", TD2FD[i].re, TD2FD[i].im);
            }
            Console.WriteLine();
        }
    }

    //定义复数
    public class Complex
    {
        public float re;//实数部
        public float im;//虚数部

        // 幅值
        public double Amplitude
        {
            get {
                return Math.Sqrt(re*re + im*im);
            }
        }

        // 相位
        public double Phase
        {
            get {
                return Math.Atan2(im, re);
            }
        }

        public static Complex operator +(Complex lhs, Complex rhs)
        {
            Complex result = new Complex();
            result.re = lhs.re + rhs.re;
            result.im = lhs.im + rhs.im;
            return result;
        }

        public static Complex operator -(Complex lhs, Complex rhs)
        {
            Complex result = new Complex();
            result.re = lhs.re - rhs.re;
            result.im = lhs.im - rhs.im;
            return result;
        }

        public static Complex operator *(Complex lhs, Complex rhs)
        {
            Complex result = new Complex();
            result.re = lhs.re * rhs.re - lhs.im * rhs.im;
            result.im = lhs.re * rhs.im + lhs.im * rhs.re;
            return result;
        }

        public static Complex operator *(float lhs, Complex rhs)
        {
            Complex result = new Complex();
            result.re = lhs * rhs.re;
            result.im = lhs * rhs.im;
            return result;
        }

        public static Complex operator *(Complex lhs, float rhs)
        {
            Complex result = new Complex();
            result.re = lhs.re * rhs;
            result.im = lhs.im * rhs;
            return result;
        }
    }

    public class Complex2D
    {
        private List<Complex[]> rows = new List<Complex[]>();
        private List<Complex[]> columns = new List<Complex[]>();
        private int m_width;
        private int m_height;

        public Complex2D(int width, int height)
        {
            m_width = width;
            m_height = height;
            for (int i = 0; i < height; i++)
                rows.Add(new Complex[width]);
            for (int i = 0; i < width; i++)
                columns.Add(new Complex[height]);
        }

        public int Width { get { return m_width; } }
        public int Height { get { return m_height; } }

        public Complex[] GetRow(int i)
        {
            return rows[i];
        }

        public Complex[] GetColumn(int i)
        {
            return columns[i];
        }

        public void SetRow(int i, Complex[] src)
        {
            rows[i] = src;
        }

        public void SetColumn(int i, Complex[] src)
        {
            columns[i] = src;
        }

        public void SetComplex(int i, int j, Complex src)
        {
            rows[i][j] = src;
            columns[j][i] = src;
        }

        public void SetComplexs(Complex[][] src)
        {
            for (int i=0; i<src.Length; i++)
            {
                Complex[] row = src[i];
                for (int j = 0; j < row.Length; j++)
                    SetComplex(i, j, row[j]);
            }
        }

        public void Print()
        {
            for (int i=0; i<rows.Count; i++)
            {
                Complex[] row = rows[i];
                for (int j = 0; j < row.Length; j++)
                    Console.Write("{0:G} ", row[j].re.ToString().PadRight(5));
                Console.WriteLine();
            }
            Console.WriteLine();
        }
    }
}


运行测试
111111.png 


//频谱分析窗函数类型
public enum FFTWindow
{
	//
	// 矩形窗 (使用最多的窗)
	// W[n] = 1.0.
	Rectangular = 0,
	//
	// 三角窗
	// W[n] = TRI(2n/N).
	Triangle = 1,
	//
	// 汉宁窗(余弦窗)
	// W[n] = 0.54 - (0.46 * COS(n/N) ).
	Hamming = 2,
	//
	// 海明窗(升余弦窗)
	// W[n] = 0.5 * (1.0 - COS(n/N) ).
	Hanning = 3,
	//
	// 布拉克曼
	// W[n] = 0.42 - (0.5 * COS(nN) ) + (0.08 * COS(2.0 * nN) ).
	Blackman = 4,
	//
	// 哈布斯窗
	// W[n] = 0.35875 - (0.48829 * COS(1.0 * nN)) + (0.14128 * COS(2.0 * nN)) - (0.01168 * COS(3.0 * n/N)).
	BlackmanHarris = 5
}


更多示例: Matlib——二维傅里叶变换

标签: Algorithms

« C#调用Lua函数 | Lnaguage Intergrated Query(Linq) 集成查询语言»
Powered by emlog  蜀ICP备18021003号-1   sitemap

川公网安备 51019002001593号