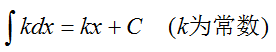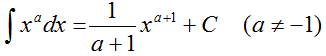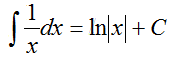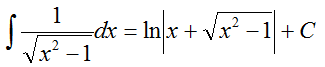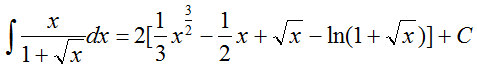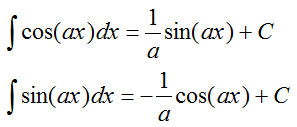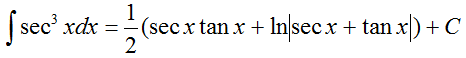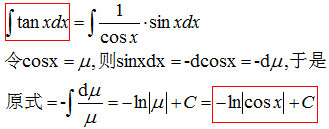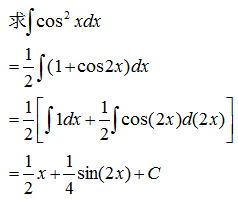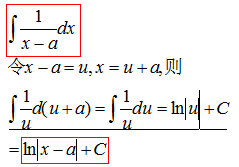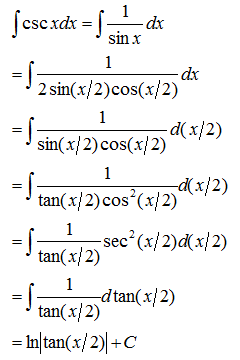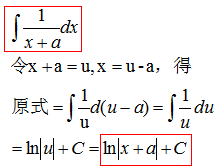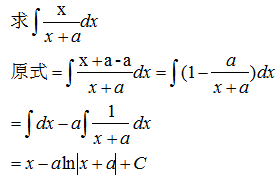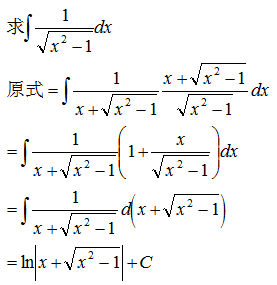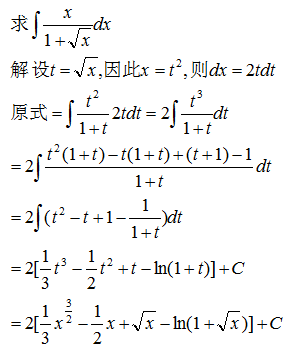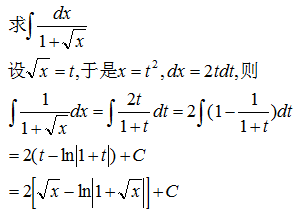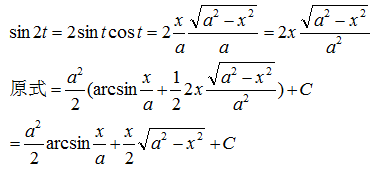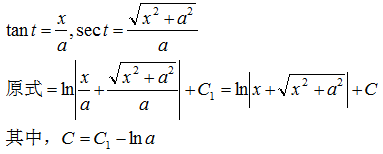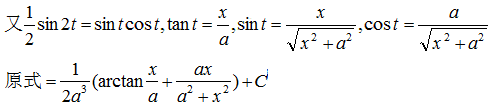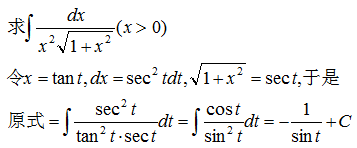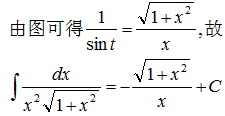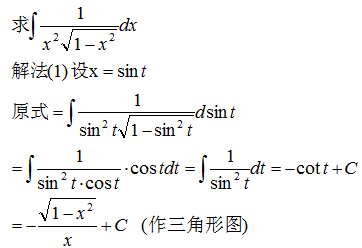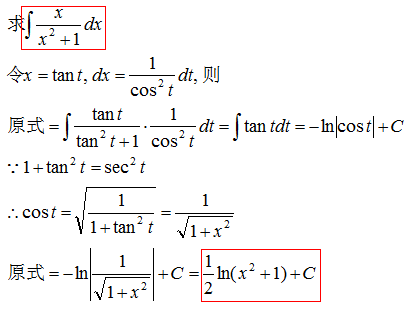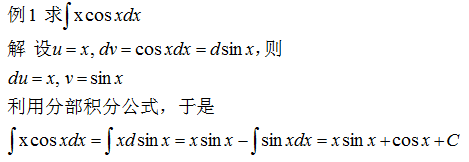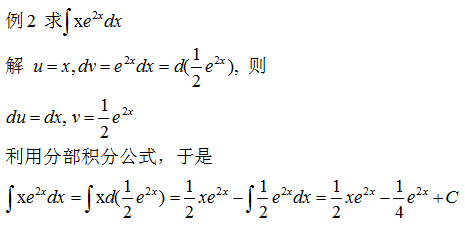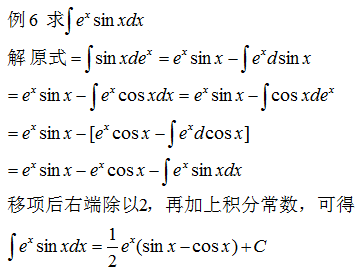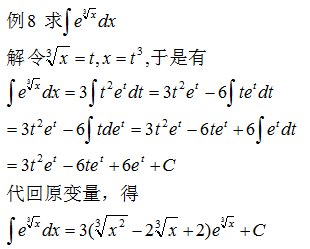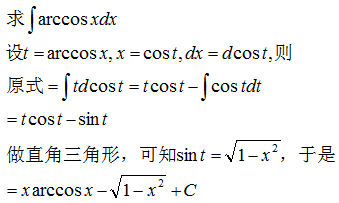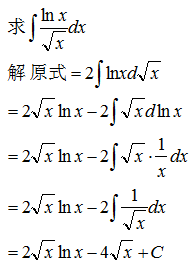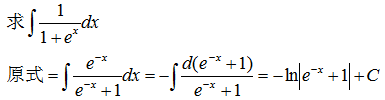高等数学——不定积分
作者:追风剑情 发布于:2021-7-31 10:24 分类:Algorithms
一、不定积分
定义1 已知函数f(x)在某区间I上有定义,如果存在函数F(x),使得在I上任何一点x都有 F'(x)=f(x) 或 dF(x)=f(x)dx 则称F(x)为f(x)在I上的一个原函数。
' : 代表对F(x)求导(F'(x))
d: 代表对F(x)求导(dF(x)),dx代表积分变量是x
f(x)dx: f(x)是导函数,dx表示求导变量是x
因为 (F(x) + C)' = f(x),C为常数,所以只要f(x)有一个原函数,它就有无穷多个原函数。因此,F(x) + C 是 f(x) 的原函数的一般表达式,其中 C 为任意常数。
如果F(x)和G(x)都是f(x)在区间I上的原函数,则G(x)和F(x)之间只相差一个常数。
[G(x) - F(x)]' = G'(x) - F'(x) = f(x) - f(x) = 0
G(x) - F(x) = C
G(x) = F(x) + C
定义2 在区间I上,如果函数F(x)是函数f(x)的一个原函数,则f(x)的全体原函数F(x)+C称为f(x)的不定积分,记为 ∫ƒ(x)dx=F(x)+C,其中,"∫" 称为积分号,ƒ(x) 称为被积函数,ƒ(x)dx 称为被积表达式,x 称为积分变量,C 称为积分常量。
由定义2可知,要求函数f(x)的不定积分,只要求出f(x)的任何一个原函数F(x),再加上一个任意常数即可。
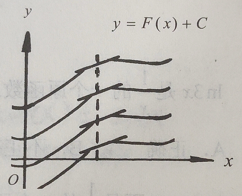
不定积分的几何意义
在直角坐标系中,f(x)的任意一个原函数F(x)的图形,称为f(x)的一条积分曲线,其方程是 y=F(x)。这样,不定积分∫ƒ(x)dx在几何上表示一族积分曲线 y=F(x)+C,称为f(x)的积分曲线族。积分曲线族中任何一条曲线,都可以由y=F(x)沿y轴平移一段C得到(如图)。因此,在横坐标x相同的点处,所有积分曲线的切线彼此平行,这些曲线具有相同的斜率F'(x)=f(x)。
二、不定积分的性质和基本积分公式
求不定积分的运算称为积分运算或积分法,由不定积分的定义,积分运算是微分运算的逆运算,从而容易得出它们之间具有如下关系:
性质1
(1) [∫ƒ(x)dx]' = f(x) 或 d∫ƒ(x)dx = ƒ(x)dx
(2) ∫ƒ'(x)dx = ƒ(x) + C 或 ∫dƒ(x) = ƒ(x) + C
证 设F(x)是f(x)的一个原函数,则
[∫ƒ(x)dx]' = [F(x) + C]' = F'(x) = f(x)
所以(1)成立。
由于f(x)是f'(x)的一个原函数,(2)显然成立。
性质2
∫[ƒ(x) + g(x)]dx = ∫ƒ(x)dx + ∫g(x)dx
证 将上式右端对x求导,得
[∫ƒ(x)dx + ∫g(x)dx]' = [∫ƒ(x)dx]' + [∫g(x)dx]' = ƒ(x) + g(x)
这说明等式右端的导数确是左端的被积函数,因此性质2成立。
性质3
∫kƒ(x)dx = k∫ƒ(x)dx (k为非零常数)
证
左边 [∫kƒ(x)dx]' = kƒ(x)
右边 [k∫ƒ(x)dx]' = k[∫ƒ(x)dx]' = kƒ(x)
由性质2和性质3显然有:有限个函数的线性组合的积分等于积分后的线性组合,即
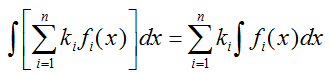
其中,ki(i=1, 2, ..., n)为不全为零的常数。
基本积分公式
以上基本积分公式,是求不定积分的基础,需要熟记。在许多情况下,被积函数不是基本积分表所列的,这时需要对被积函数进行各种恒等变形,使其可以利用不定积分的基本公式。
三、换元积分法
利用基本积分公式和不定积分的性质能够求积分的函数是非常有限的,即使像tanx与lnx这种基本初等函数的积分都不能求得。因此,有必要寻求更多的积分方法。
定理1 (第一类换元积分法)如果F'(u)=f(u),又 u=φ(x) 有连续导数。则
![]()
证 只需证明右端的导数等于左端的被积函数即可。由复合函数求导,则
![]()
定理得证。
定理1 的基本思想是:当不定积分∫g(x)dx不易求时,如果可以将被积分函数g(x)凑成g(x)=ƒ[φ(x)]φ'(x),再作代换φ(x)=u,得φ'(x)=du,于是 ∫g(x)dx=∫ƒ[φ(x)]φ'(x)dx=∫ƒ(u)du。若对新积分变量u,可以积分∫ƒ(u)du=F(u)+C,然后将u还原为u=φ(x),于是,原来的不定积分 ∫g(x)dx=∫ƒ[φ(x)]φ'(x)dx=F[φ(x)]+C
这种先 “凑” 微分式,再作代换的积分方法,叫做 凑微分法。注意用凑微分法计算不定积分通常有三个步骤:
一是凑微分(凑出 φ'(x)dx 后,被积函数中剩下部分是 φ(x) 的函数);
二是配系数;
三是利用基本积分公式(∫ƒ(u)du 要容易求出)。
求解流程:凑→换元→利用基本积分公式求解→还原积分变量
示例 1 - 凑微分法
示例 2
示例 3
示例 4
示例 5
示例 6
示例 7
示例 8
示例 9
定理 2 (第二类换元积分法) 如果
(1) x=ψ(t)单调可微,且ψ'(t)≠0
(2) g[ψ(t)]ψ'(t)具有原函数F(t)。
则
∫g(x)dx=∫g[ψ(t)]ψ'(t)dt=F(t)+C=F(ψ-1(x))+C
其中,t=ψ-1(x)是x=ψ(t)的反函数。条件(1)是为了保证x=ψ(t)的反函数t=ψ-1(x)存在,且∫g[ψ(t)]ψ'(t)dt有意义,所以此条件不能忽略。例如
![]()
定理 1 可以理解成先凑表达式,再用新变量代换,最后再套积分公式求解。
定理 2 可以理解成将变量化成表达式,再来套积分公式求解。
示例 1: 消根号
当被积函数中含有一次根式![]() 时,一般可令ax+b=tn将根号去掉。
时,一般可令ax+b=tn将根号去掉。
示例 2
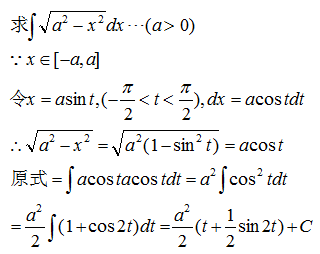
为了将最终结果表示为x的函数,由x=asint作出如图所示的直角三角形,由图可知:
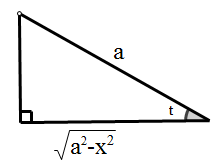
示例 3
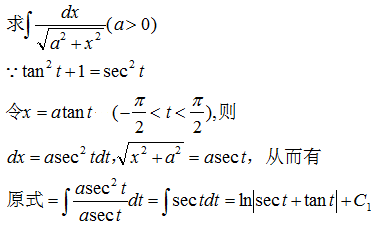
为了将最终结果表示为x的函数,由x=atant作出如图所示的直角三角形
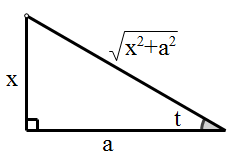
由图示可知
示例 4
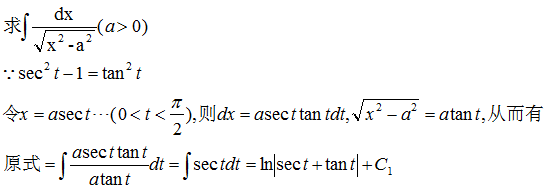
为了将最终结果表示为x的函数,由x=asect作出如图所示的直角三角形,由图示可知
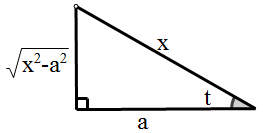
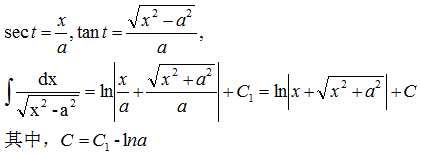
从上面的示例可以总结出:
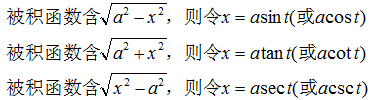
这类代换称为三角代换,它可以用来去掉被积函数中的二次根式。当然,三角代换有时也可以用于某些被积函数不含根式的积分(例如,示例 5)。
示例 5
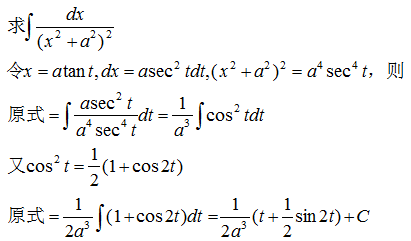
为了将最终结果表示为x的函数,由x=atant作出如图所示的直角三角形,由图示可知
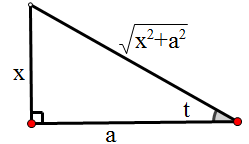
示例 6
示例 7
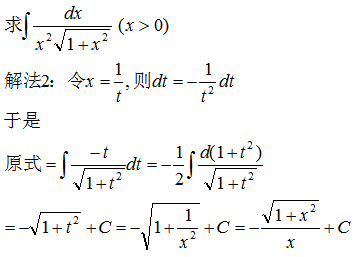
上述代换x=1/t称为倒代换。一般说来,当被积函数的分母中含有因子xn(n为自然数)时,可考虑使用倒代换。因为采用x=1/t后,xn=1/tn,dx=-(1/t2)dt,xn=1/tn乘以t2后变为1/tn-2,从而可降低xn的次数。
示例 8
三、分部积分法
分部积分法是由两个函数乘积微分法逆转而来,利用这个公式,我们有时就能把比较难求的积分∫udv转化为比较容易求的积分∫vdu来计算。所以,利用分部积分法求不定积分的原则是:
(1) 选择 u,使它的导数 u' 比 u “简单”;<
(2) 选取 dv (或v') ,使 v 容易求出;
(3) 积分 ∫vdu 较易
以下这个例子用到了换元法和分部积分公式,以及三角形做图法。
标签: Algorithms
日历
最新文章
随机文章
热门文章
分类
存档
- 2026年1月(5)
- 2025年12月(1)
- 2025年11月(1)
- 2025年9月(3)
- 2025年7月(4)
- 2025年6月(5)
- 2025年5月(1)
- 2025年4月(5)
- 2025年3月(4)
- 2025年2月(3)
- 2025年1月(1)
- 2024年12月(5)
- 2024年11月(5)
- 2024年10月(5)
- 2024年9月(3)
- 2024年8月(3)
- 2024年7月(11)
- 2024年6月(3)
- 2024年5月(9)
- 2024年4月(10)
- 2024年3月(11)
- 2024年2月(24)
- 2024年1月(12)
- 2023年12月(3)
- 2023年11月(9)
- 2023年10月(7)
- 2023年9月(2)
- 2023年8月(7)
- 2023年7月(9)
- 2023年6月(6)
- 2023年5月(7)
- 2023年4月(11)
- 2023年3月(6)
- 2023年2月(11)
- 2023年1月(8)
- 2022年12月(2)
- 2022年11月(4)
- 2022年10月(10)
- 2022年9月(2)
- 2022年8月(13)
- 2022年7月(7)
- 2022年6月(11)
- 2022年5月(18)
- 2022年4月(29)
- 2022年3月(5)
- 2022年2月(6)
- 2022年1月(8)
- 2021年12月(5)
- 2021年11月(3)
- 2021年10月(4)
- 2021年9月(9)
- 2021年8月(14)
- 2021年7月(8)
- 2021年6月(5)
- 2021年5月(2)
- 2021年4月(3)
- 2021年3月(7)
- 2021年2月(2)
- 2021年1月(8)
- 2020年12月(7)
- 2020年11月(2)
- 2020年10月(6)
- 2020年9月(9)
- 2020年8月(10)
- 2020年7月(9)
- 2020年6月(18)
- 2020年5月(4)
- 2020年4月(25)
- 2020年3月(38)
- 2020年1月(21)
- 2019年12月(13)
- 2019年11月(29)
- 2019年10月(44)
- 2019年9月(17)
- 2019年8月(18)
- 2019年7月(25)
- 2019年6月(25)
- 2019年5月(17)
- 2019年4月(10)
- 2019年3月(36)
- 2019年2月(35)
- 2019年1月(28)
- 2018年12月(30)
- 2018年11月(22)
- 2018年10月(4)
- 2018年9月(7)
- 2018年8月(13)
- 2018年7月(13)
- 2018年6月(6)
- 2018年5月(5)
- 2018年4月(13)
- 2018年3月(5)
- 2018年2月(3)
- 2018年1月(8)
- 2017年12月(35)
- 2017年11月(17)
- 2017年10月(16)
- 2017年9月(17)
- 2017年8月(20)
- 2017年7月(34)
- 2017年6月(17)
- 2017年5月(15)
- 2017年4月(32)
- 2017年3月(8)
- 2017年2月(2)
- 2017年1月(5)
- 2016年12月(14)
- 2016年11月(26)
- 2016年10月(12)
- 2016年9月(25)
- 2016年8月(32)
- 2016年7月(14)
- 2016年6月(21)
- 2016年5月(17)
- 2016年4月(13)
- 2016年3月(8)
- 2016年2月(8)
- 2016年1月(18)
- 2015年12月(13)
- 2015年11月(15)
- 2015年10月(12)
- 2015年9月(18)
- 2015年8月(21)
- 2015年7月(35)
- 2015年6月(13)
- 2015年5月(9)
- 2015年4月(4)
- 2015年3月(5)
- 2015年2月(4)
- 2015年1月(13)
- 2014年12月(7)
- 2014年11月(5)
- 2014年10月(4)
- 2014年9月(8)
- 2014年8月(16)
- 2014年7月(26)
- 2014年6月(22)
- 2014年5月(28)
- 2014年4月(15)
友情链接
- Unity官网
- Unity圣典
- Unity在线手册
- Unity中文手册(圣典)
- Unity官方中文论坛
- Unity游戏蛮牛用户文档
- Unity下载存档
- Unity引擎源码下载
- Unity服务
- Unity Ads
- wiki.unity3d
- Visual Studio Code官网
- SenseAR开发文档
- MSDN
- C# 参考
- C# 编程指南
- .NET Framework类库
- .NET 文档
- .NET 开发
- WPF官方文档
- uLua
- xLua
- SharpZipLib
- Protobuf-net
- Protobuf.js
- OpenSSL
- OPEN CASCADE
- JSON
- MessagePack
- C在线工具
- 游戏蛮牛
- GreenVPN
- 聚合数据
- 热云
- 融云
- 腾讯云
- 腾讯开放平台
- 腾讯游戏服务
- 腾讯游戏开发者平台
- 腾讯课堂
- 微信开放平台
- 腾讯实时音视频
- 腾讯即时通信IM
- 微信公众平台技术文档
- 白鹭引擎官网
- 白鹭引擎开放平台
- 白鹭引擎开发文档
- FairyGUI编辑器
- PureMVC-TypeScript
- 讯飞开放平台
- 亲加通讯云
- Cygwin
- Mono开发者联盟
- Scut游戏服务器引擎
- KBEngine游戏服务器引擎
- Photon游戏服务器引擎
- 码云
- SharpSvn
- 腾讯bugly
- 4399原创平台
- 开源中国
- Firebase
- Firebase-Admob-Unity
- google-services-unity
- Firebase SDK for Unity
- Google-Firebase-SDK
- AppsFlyer SDK
- android-repository
- CQASO
- Facebook开发者平台
- gradle下载
- GradleBuildTool下载
- Android Developers
- Google中国开发者
- AndroidDevTools
- Android社区
- Android开发工具
- Google Play Games Services
- Google商店
- Google APIs for Android
- 金钱豹VPN
- TouchSense SDK
- MakeHuman
- Online RSA Key Converter
- Windows UWP应用
- Visual Studio For Unity
- Open CASCADE Technology
- 慕课网
- 阿里云服务器ECS
- 在线免费文字转语音系统
- AI Studio
- 网云穿
- 百度网盘开放平台
- 迅捷画图
- 菜鸟工具
- [CSDN] 程序员研修院
- 华为人脸识别
- 百度AR导航导览SDK
- 海康威视官网
- 海康开放平台
- 海康SDK下载
- git download
- Open CASCADE
- CascadeStudio
交流QQ群
-
Flash游戏设计: 86184192
Unity游戏设计: 171855449
游戏设计订阅号