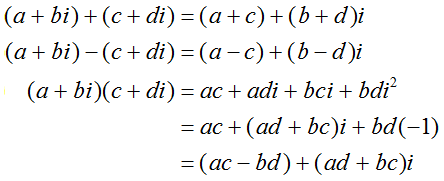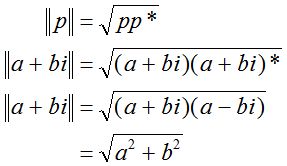鸟语天空

四元数(Quaternion)

作者：追风剑情 发布于：2021-7-23 16:13 分类：Algorithms

一、四元数记法

一个四元数包含一个标量分量和一个3D向量分量。经常记标量分量为w，记向量分量为单一的v或分开的x, y, z。两种记法分别如下：

[w, v]
[w, (x, y, z)]

在某些情况下，用v这样的短记法更方便，但另一些情况下，“扩展”的记法会更清楚。

也可以将四元数竖着写，有时这会使等式的格式一目了然。“行”或“列”四元数没有明显的区别。

二、四元数与复数

复数对(a, b)定义了数a+bi，i是所谓的虚数，满足i²=-1，a称作实部，b称作虚部。任意实数k都能表示为复数(k, 0)=k+0i。

复数能够相加、相减、相乘：

三、共轭复数

通过使虚部变负，还能够计算复数的共轭。记法如下：

p=(a+bi)

p*=(a-bi)

四、求复数的模

还能够计算复数的模。这个运算的记法和解释与实数的绝对值类似。实际上，如果将实数表示成复数，它们将产生相同的结果。公式如下：

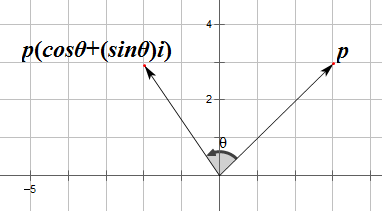
复数集存在于一个2D平面上，可以认为这个平面有两个轴：实轴和虚轴。这样，就能将复数(x, y)解释为2D向量。用这种方法解释复数时，它们能用来表达平面中的旋转(虽然这走了一个弯路)。看看复数p绕原点旋转角度θ的情况。

在平面中旋转复数

为了进行这个旋转，引入第二个复数q=(cosθ, sinθ)。现在，旋转后的复数p'能用复数乘法计算出来：

p = x + yi
q = cosθ + isinθ
p' = pq
   =(x+yi)(cosθ+isinθ)
   =(xcosθ-ysinθ)+(xsinθ+ycosθ)i

当然，从上式来看，引入复数q和用2×2旋转矩阵达到的效果是一样的，但复数提供了另一种有趣的记法。后面，我们将以同样的方法在3D中使用四元数。

四元数扩展了复数系统，它使用三个虚部 i，j，k。它们之间的关系如下： $$ \begin{flalign} &i^2=j^2=k^2=-1 \quad (根据定义)& \\ &ij=k,ji=-k \quad\quad (叉乘)& \\ &jk=i,kj=-i \quad\quad (叉乘)& \\ &ki=j,ik=-j \quad\quad (叉乘)& \end{flalign} $$

  一个四元数 [w, (x, y, z)] 定义了复数 w+xi+yj+zk。我们马上将会看到，很多标准复数的性质都能应用到四元数上。更重要的是，和复数能用来旋转2D中的向量类似，四元数也能用来旋转3D中的向量。

五、四元数和轴-角对

  欧拉证明了一个旋转序列等价于单个旋转。因此，3D中的任意角位移都能表示为绕单一轴的单一旋转（这里的轴是一般意义上的轴，不要和笛卡尔坐标轴混淆。显然，旋转轴的方向是任意的）。当一个方位用这种形式来描述时称作轴-角描述法（实际上，能将轴-角形式作为描述方位的第四种表达方式。但是，轴-角对很少用到，经常被欧拉角或四元数替代）。

  设 n 为旋转轴。对于旋转轴来说长度并不重要，将 n 定义为单位长度会比较方便。根据左手或右手法则，n 的方向定义了哪边将被认为是旋转“正”方向。设 θ 为绕轴旋转的量。因此，轴-角对 (n, θ) 定义了一个角位移：绕 n 指定的轴旋转 θ 角。

  四元数能被解释为角位移的轴-角对方式。然而，n 和 θ 不是直接存储在四元数的四个数中——那样太简单了！它们的确在四元素里，但不是那么直接。下列公式给出了四元数中的数和 n，θ 的关系，两种四元数记法都被使用了。

$ \begin{align} \mathbf{q}&=[cos(θ/2) \quad sin(θ/2)\mathbf{n}] \\ &=[cos(θ/2) \quad sin(θ/2)\mathbf{n}_x \quad sin(θ/2)\mathbf{n}_y \quad sin(θ/2)\mathbf{n}_z] \end{align} $

六、负四元数

四元数能求负。做法很直接：将每个分量都变负。

$ \begin{flalign} \mathbf{-q}&=-[w \quad (x \quad y \quad z)]=[-w \quad (-x \quad -y \quad -z)] \\ &=-[w \quad \mathbf{v}]=[-w \quad -\mathbf{v}] \end{flalign} $

从上面的公式可以看出，当q取负值时，旋转角和旋转轴都反向了，所以q和-q代表的实际角位移是相同的。

cos(θ/2)与sin(θ/2)，当θ增加$360^\circ$的奇数倍时，分量的符号将取反。当θ增加$360^\circ$的偶数倍时，符号不变。

q和-q代表的实际角位移是相同的。如果我们将θ加上$360^\circ$的倍数，不会改变q代表的角位移，但它使q的四个分量都变负了。因此，3D中的任意角位移都有两种不同的四元数表示方法，它们互相为负。

七、单位四元数

  几何上，存在两个“单位”四元数，它们代表没有角位移：[1, 0]和[-1, 0]（注意粗体0，它们代表零向量）。当θ是$360^\circ$的偶数倍时，有第一种形式，cos(θ/2)=1；θ是$360^\circ$的奇数倍时，有第二种形式，cos(θ/2)=-1。在两种情况下，都有sin(θ/2)=0，所以n的值无关紧要。它的意义在于：

  当旋转角θ是$360^\circ$的整数倍时，方位并没有改变，并且旋转轴也是无关紧要的。

  数学上，实际只有一个单位四元数：[1, 0]。用任意四元数q乘以单位四元数[1, 0]，结果仍是q。任意四元数q乘以另一个“几何单位”四元数[-1, 0]时得到-q。几何上，因为q和-q代表的角位移相同，可认为结果是相同的。但在数学上，q和-q不相等，所以[-1, 0]并不是“真正”的单位四元数。

八、四元数的模

和复数一样，四元数也有模。记法和公式都与向量的类似，如公式所示。 \begin{flalign} |\mathbf{q}|&=|\left[w\quad (x\quad y\quad z)\right]|=\sqrt{w^2+x^2+y^2+z^2} &\\ &=|[w\quad \mathbf{v}]|=\sqrt{w^2+|\mathbf{v}|^2} &\\ \end{flalign}

让我们看看它的几何意义。代入$\theta$和n，可得到： \begin{flalign} |\mathbf{q}|&=|[w\quad \mathbf{v}]| &\\ &=\sqrt{w^2+ |\mathbf{v}|^2} &\\ &=\sqrt{cos^2(θ/2) + (sin(θ/2)|\mathbf{n}|)^2} \end{flalign} n为单位向量，所以： \begin{flalign} |\mathbf{q}|&=\sqrt{cos^2(θ/2) + sin^2(θ/2)|\mathbf{n}|^2} &\\ &=\sqrt{cos^2(θ/2) + sin^2(θ/2)(1)} &\\ &=\sqrt{cos^2(θ/2) + sin^2(θ/2)} &\\ \end{flalign} 应用三角公式$sin^2x+con^2x=1$，得到： \begin{flalign} |\mathbf{q}|&=\sqrt{cos^2(θ/2) + sin^2(θ/2)}=\sqrt{1}=1 &\\ \end{flalign} 如果为了用四元数来表示方位，我们仅使用符合这个规则的单位四元数。

九、四元数的共轭

四元数的共轭记作q^*，可通过让四元数的向量部分变负来获得。 \begin{flalign} \mathbf{q}^*&=\left[\begin{array}{l} w & \mathbf{v} \end{array}\right]^*=\left[\begin{array}{l} w & -\mathbf{v} \end{array}\right] &\\ &=\left[\begin{array}{l} w & (x & y & z) \end{array}\right]^*=\left[\begin{array}{l} w & (-x & -y & -z) \end{array}\right] &\\ \end{flalign}

共轭非常有趣，因为q和q^*代表相反的角位移。很容易验证这种说法，使v变负，也就是使旋转轴反向，它颠倒了我们所认为的旋转正方向。因此，q绕轴旋转θ角，而q^*沿相反的方向旋转相同的角度。

针对我们的目的而言，四元数的共轭可以有另一种定义：w变负，v不变。这使旋转角度变负，而不是通过翻转旋转轴来颠倒正方向。这和公式给出的定义等价（至少对于我们的目的是这样的），并提供了一种稍微快一点的实现和更为直观的几何解释。但对于复数，术语“共轭”有其特殊含义，因此我们保持原定义不变。

十、四元数的逆

四元数的逆记作q^-1，定义为四元数的共轭除以它的模。 \begin{flalign} &\mathbf{q}^{-1}=\frac{\mathbf{q}^*}{\mathbf{|q|}} &\\ \end{flalign} 上面的公式为四元数逆的正式定义，但我们只使用单位四元数，所以四元数的逆和共轭是相等的。

四元数的逆和实数的倒数有着有趣的对应关系。对于实数a，它的逆a^-1为1/a，从另一方面说，a(a^-1)=a^-1a=1。四元数的逆也有同样的性质。一个四元数q乘以它的逆q^-1，即可得到单位四元数[1, 0]。

十一、四元数乘法(叉乘)

四元数根据复数解释来相乘，如下： \begin{flalign} &(w_1+x_1i+y_1j+z_1k)(w_2+x_2i+y_2j+z_2k) &\\ &=w_1w_2+w_1x_2i+w_1y_2j+w_1z_2k &\\ &\quad+x_1w_2i+x_1x_2i^2+x_1y_2ij+x_1z_2ik &\\ &\quad+y_1w_2j+y_1x_2ji+y_1y_2j^2+y_1z_2jk &\\ &\quad+z_1w_2k+z_1x_2ki+z_1y_2kj+z_1z_2k^2 &\\ &=w_1w_2+w_1x_2i+w_1y_2j+w_1z_2k &\\ &\quad+x_1w_2i+x_1x_2(-1)+x_1y_2ij+x_1z_2ik &\\ &\quad+y_1w_2j+y_1x_2ji+y_1y_2(-1)+y_1z_2jk &\\ &\quad+z_1w_2k+z_1x_2ki+z_1y_2kj+z_1z_2(-1) &\\ &=w_1w_2-x_1x_2-y_1y_2-z_1z_2 &\\ &\quad+(w_1x_2+x_1w_2+y_1z_2-z_1y_2)i &\\ &\quad+(w_1y_2+y_1w_2+z_1x_2-x_1z_2)j &\\ &\quad+(w_1z_2+z_1w_2+x_1y_2-y_1x_2)k &\\ &=\left[\begin{array}{l} w_1w_2-\mathbf{v}_1\cdot\mathbf{v}_2 & w_1\mathbf{v}_2+w_2\mathbf{v}_1+\mathbf{v}_1×\mathbf{v}_2 \end{array}\right] &\\ \end{flalign} 这导出了四元数乘法的标准定义，下面以两种四元数记法给出。 \begin{flalign} &\left[\begin{array}{l}w_1 & (x_1 & y_1 & z_1)\end{array}\right]\left[\begin{array}{l}w_2 & (x_2 & y_2 & z_2)\end{array}\right] &\\ &=\left[ \begin{array}{l} \quad w_1w_2-x_1x_2-y_1y_2-z_1z_2 \\ \left( \begin{array}{l} w_1x_2+x_1w_2+z_1y_2-y_1z_2 \\ w_1y_2+y_1w_2+x_1z_2-z_1x_2 \\ w_1z_2+z_1w_2+y_1x_2-x_1y_2 \end{array} \right) \end{array} \right] \end{flalign} \begin{flalign} &\left[ \begin{array}{l} w_1 & \mathbf{v}_1 \end{array} \right] \left[ \begin{array}{l} w_2 & \mathbf{v}_2 \end{array} \right] &\\ &=\left[\begin{array}{l} w_1w_2-\mathbf{v}_1\cdot\mathbf{v}_2 & w_1\mathbf{v}_2+w_2\mathbf{v}_1+\mathbf{v}_2×\mathbf{v}_1 \end{array}\right] &\\ \end{flalign}

不用为四元数叉乘使用乘号，“行”或“列”四元数也没有什么区别。

四元数叉乘满足结合律，但不满足交换律。 \begin{flalign} &(\mathbf{ab})\mathbf{c}=\mathbf{a}(\mathbf{bc}) &\\ &\mathbf{ab}≠\mathbf{ba} &\\ \end{flalign}

现在看看两个四元数叉乘的模： \begin{flalign} &|\mathbf{q}_1\mathbf{q}_2|=|\left[\begin{array}{l}w_1 & (x_1 & y_1 & z_1) \end{array}\right]\left[\begin{array}{l} w_2 & (x_2 & y_2 & z_2)\end{array}\right]| &\\ &=\left|\left[\begin{array}{l} \quad w_1w_2-x_1x_2-y_1y_2-z_1z_2 \\ \left( \begin{array}{l} w_1x_2+x_1w_2+z_1y_2-y_1z_2 \\ w_1y_2+y_1w_2+x_1z_2-z_1x_2 \\ w_1z_2+z_1w_2+y_1x_2-x_1y_2 \end{array} \right) \end{array}\right]\right| &\\ &=\sqrt{ \begin{array}{l} (w_1w_2-x_1x_2-y_1y_2-z_1z_2)^2 \\ +(w_1x_2+x_1w_2+z_1y_2-y_1z_2)^2 \\ +(w_1y_2+y_1w_2+x_1z_2-z_1x_2)^2 \\ +(w_1z_2+z_1w_2+y_1x_2-x_1y_2)^2 \end{array} } &\\ \end{flalign} 展开并合同类项（因为这个步骤很冗长所以我们就把它省略了）得到公式： \begin{flalign} |\mathbf{q}_1\mathbf{q}_2|&=\sqrt{ \begin{array}{l} w_1^2w_2^2+x_1^2x_2^2+y_1^2y_2^2+z_1^2z_2^2 \\ +w_1^2x_2^2+x_1^2w_2^2+z_1^2y_2^2+y_1^2z_2^2 \\ +w_1^2y_2^2+y_1^2w_2^2+x_1^2z_2^2+z_1^2x_2^2 \\ +w_1^2z_2^2+z_1^2w_2^2+y_1^2x_2^2+x_1^2y_2^2 \end{array} } &\\ &=\sqrt{ \begin{array}{l} w_1^2(w_2^2+x_2^2+y_2^2+z_2^2) \\ +x_1^2(w_2^2+x_2^2+y_2^2+z_2^2) \\ +y_1^2(w_2^2+x_2^2+y_2^2+z_2^2) \\ +z_1^2(w_2^2+x_2^2+y_2^2+z_2^2) \end{array} } &\\ &=\sqrt{ (w_1^2+x_1^2+y_1^2+z_1^2)(w_2^2+x_2^2+y_2^2+z_2^2) } \end{flalign} 最后，应用四元数模的定义得到公式： \begin{flalign} |\mathbf{q}_1\mathbf{q}_2|&=\sqrt{(w_1^2+x_1^2+y_1^2+z_1^2)(w_2^2+x_2^2+y_2^2+z_2^2)} &\\ &=\sqrt{|\mathbf{q}_1|^2|\mathbf{q}_2|^2} &\\ &=|\mathbf{q}_1||\mathbf{q}_2| \end{flalign} 四元数乘积的模等于模的乘积。

因此，四元数乘积的模等于模的乘积。这个结论非常重要，因为它保证了两个单位四元数相乘的结果还是单位四元数。

四元数乘积的逆等于各个四元数的逆以相反的顺序相乘。 \begin{flalign} &(\mathbf{ab})^{-1}=\mathbf{b}^{-1}\mathbf{a}^{-1} &\\ &(\mathbf{q}_1\mathbf{q}_2\cdots\mathbf{q}_{n-1}\mathbf{q}_n)^{-1}=\mathbf{q}_n^{-1}\mathbf{q}_{n-1}^{-1}\cdots\mathbf{q}_2^{-1}\mathbf{q}_1^{-1} &\\ \end{flalign}

现在到了四元数非常有用的性质。让我们“扩展”一个标准3D点(x, y, z)到四元数空间，通过定义四元数p=[0, (x, y, z)]即可（当然，在一般情况下，p不会是单位四元数）。设q为我们讨论的旋转四元数形式[cos(θ/2), nsin(θ/2)]，n为旋转轴，单位向量；θ为旋转角。您会惊奇地发现，执行下面的乘法可以使3D点p绕n旋转： \begin{flalign} &\mathbf{p}^{\prime}=\mathbf{q}\mathbf{p}\mathbf{q}^{-1} &\\ \end{flalign} 四元数p'中的(x,y,z)分量即为旋转后的3D向量。

我们可以证明这个等式，通过展开乘法，代入n和θ，然后和旋转矩阵公式比较。事实上，很多书正是从这里开始推导四元数向矩阵形式转换的公式。

四元数乘法的优势就在于能连接多次旋转，这和矩阵乘法的效果一样。

让我们来看看多次旋转的情况。将点p用一个四元数a旋转然后再用另一个四元数b旋转： \begin{flalign} \mathbf{p}^{\prime}&=\mathbf{b}(\mathbf{a}\mathbf{p}\mathbf{a}^{-1})\mathbf{b}^{-1} &\\ &=(\mathbf{b}\mathbf{a})\mathbf{p}(\mathbf{a}^{-1}\mathbf{b}^{-1}) &\\ &=(\mathbf{b}\mathbf{a})\mathbf{p}(\mathbf{b}\mathbf{a})^{-1} &\\ \end{flalign}

注意，先进行a旋转再进行b旋转等价于执行乘积ba代表的单一旋转。因此，四元数乘法能用来连接多次旋转，这和矩阵乘法的效果一样。根据四元数乘法的标准定义，这个旋转是以从右向左的顺序发生的。这非常不幸，因为它迫使我们以“由里向外”的顺序连接多次旋转，这和以矩阵形式作同样的运算是不同的（至少在使用行向量时是不同的）。

针对公式所导致的“顺序颠倒”问题，我们将违背标准定义，以相反的运算顺序来定义四元数乘法。注意，仅仅向量叉乘部分受到了影响。 \begin{flalign} &\left[\begin{array}{l}w_1 & (x_1 & y_1 & z_1)\end{array}\right]\left[\begin{array}{l}w_2 & (x_2 & y_2 & z_2)\end{array}\right] &\\ &=\left[ \begin{array}{l} \quad w_1w_2-x_1x_2-y_1y_2-z_1z_2 \\ \left( \begin{array}{l} w_1x_2+x_1w_2+y_1z_2-z_1y_2 \\ w_1y_2+y_1w_2+z_1x_2-x_1z_2 \\ w_1z_2+z_1w_2+x_1y_2-y_1x_2 \end{array} \right) \end{array} \right] \end{flalign} \begin{flalign} &\left[ \begin{array}{l} w_1 & \mathbf{v}_1 \end{array} \right] \left[ \begin{array}{l} w_2 & \mathbf{v}_2 \end{array} \right] &\\ &=\left[\begin{array}{l} w_1w_2-\mathbf{v}_1\cdot\mathbf{v}_2 & w_1\mathbf{v}_2+w_2\mathbf{v}_1+\mathbf{v}_1\cdot\mathbf{v}_2 \end{array}\right] &\\ \end{flalign}

这并没有改变四元数的基本性质和用v、θ的几何解释，仍然能用四元数乘法来直接旋转向量，惟一不同的是，根据我们的定义，将四元数放在向量右边，而把它的逆放在向量的左边： \begin{flalign} &\mathbf{p}^{\prime}=\mathbf{q}^{-1}\mathbf{p}\mathbf{q} &\\ \end{flalign} 能看到下面这个表达了多个旋转连接的等式，它是自左向右的，与旋转发生的顺序一致： \begin{flalign} &\mathbf{p}^{\prime}=\mathbf{b}^{-1}(\mathbf{a}^{-1}\mathbf{p}\mathbf{a})\mathbf{b} &\\ &=(\mathbf{b}^{-1}\mathbf{a}^{-1})\mathbf{p}(\mathbf{a}\mathbf{b}) &\\ &=(\mathbf{a}\mathbf{b})^{-1}\mathbf{p}(\mathbf{a}\mathbf{b}) &\\ \end{flalign} 利用修改后的四元数乘法定义更方便用程序实现四元数类。

十二、四元数“差”

  利用四元数的乘法和逆，就能够计算两个四元数的“差”。“差”被定义为一个方位到另一个方位的角位移。换句话说，给定方位a和b，能够计算从a到旋转到b的角位移d。用四元数等式更加紧凑地表示为： \begin{flalign} &\mathbf{a}\mathbf{d}=\mathbf{b} &\\ \end{flalign}

  (这里使用我们的更加直观的四元数乘法定义，旋转的顺序对应于从左向右乘法的顺序。)现在来求d。如果等式中的变量为标量，那么就可以简单的除以a。但是，不能除以四元数，只能乘它们。也许乘以它的逆能达到想要的效果！两边同时左乘a^-1（必须注意，四元数乘法不满足交换律）： \begin{flalign} &\mathbf{a}^{-1}(\mathbf{a}\mathbf{d})=\mathbf{a}^{-1}\mathbf{b} &\\ &(\mathbf{a}^{-1}\mathbf{a})\mathbf{d}=\mathbf{a}^{-1}\mathbf{b} &\\ &\left[\begin{array}{l}1 & \mathbf{0} \end{array}\right]\mathbf{d}=\mathbf{a}^{-1}\mathbf{b} &\\ &\mathbf{d}=\mathbf{a}^{-1}\mathbf{b} &\\ \end{flalign}

现在，我们就有了求得代表一个方位到另一个方位角位移的四元数的方法。

数学上，两个四元数之间的角度“差”更类似于“除”，而不是真正的“差”（减法）。

十三、四元数点乘

四元数也有点乘运算。它的记法、定义和向量点乘非常类似： \begin{flalign} \mathbf{q}_1 \cdot \mathbf{q}_2&=\left[\begin{array}{l} w_1 & \mathbf{v}_1 \end{array}\right]\cdot\left[\begin{array}{l} w_2 & \mathbf{v}_2 \end{array}\right]=w_1w_2+\mathbf{v}_1\mathbf{v}_2 &\\ &=\left[\begin{array}{l} w_1 & (x_1 & y_1 & z_1) \end{array}\right]\cdot\left[\begin{array}{l} w_2 & (x_2 & y_2 & z_2) \end{array}\right]=w_1w_2+x_1x_2+y_1y_2+z_1z_2 &\\ \end{flalign}

注意，和向量点乘一样，其结果是标量。对于单位四元数a和b，有-1≤a•b≤1。通常我们只关心a•b的绝对值，因为a•b=-(a•-b)，所以b和-b代表相同的角位移。

四元数点乘的几何解释类似于向量点乘的几何解释。四元数点乘a•b的绝对值越大，a和b代表的角位移越“相似”。

十四、四元数的对数

首先，让我们重写四元数的定义，引入一个新的变量α，等于半角θ/2： \begin{flalign} &α=θ/2 &\\ &|\mathbf{n}|=1 &\\ \end{flalign} \begin{flalign} \mathbf{q}&=\left[\begin{array}{l} cosα & \mathbf{n}sinα \end{array}\right] &\\ &=\left[\begin{array}{l} cosα & xsinα & ysinα & zsinα \end{array}\right] &\\ \end{flalign} \begin{flalign} log\mathbf{q}&=log(\left[\begin{array}{l} cosα & \mathbf{n}sinα \end{array}\right]) &\\ &\equiv \left[\begin{array}{l} 0 & α\mathbf{n} \end{array}\right] &\\ \end{flalign} $\equiv$表示“恒等于”。注意logq的结果，它一般不是单位四元数。

十五、四元数的指数

根据定义，expp总是返回单位四元数。

四元数的对数和指数类似于它们的标量形式。回忆一下，对于标量a，有下列关系成立： \begin{flalign} &e^{lna}=a &\\ \end{flalign} 同样，四元数指数运算为四元数对数运算的逆运算： \begin{flalign} &exp(log\mathbf{q})=\mathbf{q} &\\ \end{flalign}

十六、四元数和标量相乘

四元数能与一个标量相乘，其计算方法非常直接，每个分量都乘以这个标量。给定标量k和四元数q，有如下公式： \begin{flalign} k\mathbf{q}&=k[w \quad \mathbf{v}]=[kw \quad k\mathbf{v}] &\\ &=k[w \quad (x \quad y \quad z)]=[kw \quad (kx \quad ky \quad kz)] &\\ \end{flalign} 一般不会得到单位四元数，这也是为什么在表达角位移的场合中标量乘不是那么有用的原因。

十七、四元数求幂

  四元数能作为底数，记作q^t（不要和指数运算混淆，指数运算只接受一个四元数作为参数，而四元数求幂有两个参数——四元数和指数）。四元数求幂的意义类似于实数求幂。回忆下，a⁰=1，a¹=a，a为非零标量。当t从0变到1时，a^t从1到a。四元数求幂有类似的结论：当t从0变到1，q^t从[1, 0]到q。

  这对四元数求幂非常有用，因为它可以从角位移中抽取“一部分”。例如，四元数q代表一个角位移，现在想要得到1/3这个角位移的四元数，可以这样计算：q^1/3。

  指数超出[0, 1]范围外的几何行为和预期的一样（但有一个重要的注意事项）。例如，q²代表的角位移是q的两倍。假设q代表绕x轴顺时针旋转30°，那么q²代表绕x顺时针旋转60°，q^-1/3代表绕x轴逆时针旋转10°

  上面提到的注意事项是，四元数表达角位移时使用最短圆弧，不能“绕圈”。继续上面的例子，q⁴不是预期的绕x轴顺时针旋转240°(这里应该是把q当成60°了)，而是逆时针80°。显然，向一个方向旋转240°等价于向相反的方向旋转80°，都能得到正确的“最终结果”。但是，在此基础上的进一步运算，产生的就可能不是预期的结果了。例如，(q⁴)^1/2不是q²，尽管我们感觉应该是这样。一般来说，凡是涉及到指数运算的代数公式，如(a^s)^t=a^st，对四元数都不适用。

现在，我们已经理解四元数求幂可以为我们做什么了。让我们看看它的数学定义。 \begin{flalign} &\mathbf{q}^t=exp(tlog\mathbf{q}) &\\ \end{flalign}

注意，对于标量求幂，也有类似结论： \begin{flalign} &a^t=e^{(tlna)} &\\ \end{flalign}

  不难理解为什么当t从0变到1时q^t从单位四元数变到q。注意到对数运算只是提取了轴n和角度θ；接着，和指数t进行标量乘时，结果是θ乘以t；最后，指数运算“撤消”了对数运算，从tθ和n重新计算w和v。上面给出的定义就是标准的数学定义，在理论上非常完美，但直接转换到代码却是很复杂的。下面的程序清单所示代码展示了怎样计算q^t的值。

// 四元数(输入、输出)
float w,x,y,z;
// 指数
float exponent;
// 检查单位四元数的情况，避免除零
if (fabs(w) < 0.9999f) {
	// 提取半角alpha (alpha=theta/2)
	float alpha = acos(w);
	// 计算新的alpha值
	float newAlpha = alpha * exponent;
	// 计算新w值
	w = cos(newAlpha);
	// 计算新的xyz值
	float mult = sin(newAlpha) / sin(alpha);
	x *= mult;
	y *= mult;
	z *= mult;
}  

关于这些代码，需要注意的地方有：

• 首先，有必要做单位四元数的检查。因为w=±1会导致mult的计算中出现除零现象。单位四元数的任意次方还是单位四元数。因此，如果检测到输入是单位四元数，直接忽略指数直接返回原四元数即可。
• 第二，计算alpha时，使用了acos函数，它的返回值是正的角度。这并不违背一般性，任何四元数都能解释成有正方向的旋转角度。因为绕某轴的负旋转等价于绕指向相反方向的轴的正旋转。

标签: Algorithms