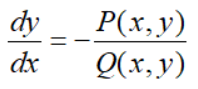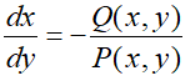一阶微分方程

作者：追风剑情发布于：2022-5-5 10:41 分类：Algorithms

本节将介绍一阶微分方程的初等解法，即把微分方程的求解问题化为积分问题进行求解。一般说来，一阶微分方程未必能用初等解法来求解，能用初等解法来求解微分方程的类型很少。但是能用初等解法来求解的微分方程在实际问题中却经常出现。因此掌握这些类型的微分方程的求解方法具有重要的实际意义。

一阶微分方程的一般形式为

(公式1)

如果由方程可以解出y'，即:

(公式2)

则称为一阶微分方程的典则形式，有时也写成

(公式3)

此时称为一阶微分方程的对称形式。在此方程中，变量x和y对称，它既可以看成是以x为自变量，y为未知函数的方程

这里Q(x,y)≠0; 也可以看成是以y为自变量，x为未知函数的方程

这里P(x,y)≠0

一、可分离变量的方程

若微分方程(2)中的函数f(x,y)可以分解为一个x的函数和一个y的函数的乘积的形式，即有 $$y'=g(x)h(y)\tag{4}$$ 则称为可分离变量的微分方程，其中g(x)，h(y)分别是x，y的连续函数。

如果h(y)≠0，可将方程(4)改写为$$\frac{dy}{h(y)}=g(x)dx$$

这样，方程两边都只包含了一个变量及其微分，即把变量分离开了。两端积分可得 $$\int\frac{dy}{h(y)}=\int{g(x)}dx$$ 我们用H(y)表示$\frac{1}{h(y)}$的一个原函数，G(x)表示g(x)的一个原函数，于是微分方程(4)的解为 $$H(y)=G(x)+C\tag{5}$$ 其中，C为任意常数。

微分方程(4)除了解(5)外，如果h(y)=0有根y=y₀，则y=y₀也是方程(4)的解。因此，在求解可分离变量的方程时，要注意这样的解。

例 1 求微分方程 $$\frac{dy}{dx}=2xy$$ 的通解。

解这是可分离变量的微分方程，分离变量后，得 $$\frac{dy}{y}=2xdx\quad(y≠0)$$ 两边积分，有 $$\int\frac{dy}{y}=\int{2xdx}$$ 于是有 $$ln|y|=x^2+C_{1}$$ $$|y|=e^{x^2+C_{1}}$$ 或 $$y=\pm{e^{C_{1}}e^{x^2}}$$ 令$C=\pm{e^{C_{1}}}$，可得所求微分方程的解为 $$y=Ce^{x^2}$$ 注意到上式的C可正可负，但C不能为零，这是因为在分离变量的过程中假定了y≠0。事实上，y=0也是原方程的解，因此，若在通解中C也可以取零，就把排除掉的解y=0也包含进去了，故原方程的通解为 $$y=Ce^{x^2}$$ 其中，C为任意常数。为了简便起见，今后遇到类似情况可同样处理，不再赘述。上面的解题过程可简化为：两边积分，得 $$ln|y|=x^2+ln|C|$$ 故通解为 $$y=Ce^{x^2}$$ 其中，C为任意常数。

例 2 求微分方程 $$(1+y^2)dx-(1+x^2)xydy=0$$ 满足初始条件$y\big|_{x=1}=1$的特解。

解将方程两端除以$x(1+x^2)(1+y^2)$, 可得 $$\frac{y}{1+y^2}dy=\frac{1}{x(1+x^2)}dx$$ 两边积分，得 $$\int\frac{y}{1+y^2}dy=\int\frac{1}{x(1+x^2)}dx$$ 由于 $$\frac{1}{x(1+x^2)}=\frac{1+x^2-x^2}{x(1+x^2)}=\frac{1}{x}-\frac{x}{1+x^2}$$ 因此有 $$\int\frac{y}{1+y^2}dy=\int\frac{1}{x}dx-\int\frac{x}{1+x^2}dx$$ 从而有 $$\frac{1}{2}ln(1+y^2)=ln|x|-\frac{1}{2}ln(1+x^2)+\frac{1}{2}lnC$$ 所求方程的通解为 $$1+y^2=\frac{Cx^2}{1+x^2}$$ 其中，C为正常数。把初始条件x=1，y=1代入通解，有 $$1+1=\frac{C}{1+1}$$ 解得C=4，故所求方程的特解为 $$1+y^2=\frac{4x^2}{1+x^2}$$

二、一阶线性方程

形如 $$a(x)\frac{dy}{dx}+b(x)y=c(x)$$ 的方程就称为一阶线性微分方程，其中 a(x) 不恒等于零。它可以变为形如 $$\frac{dy}{dx}+P(x)y=Q(x)\tag{6}$$ 的方程。以后我们主要研究这种形式的一阶线性微分方程。如果 Q(x)=0，则称方程(6)为一阶齐次线性微分方程；否则，称方程(6)为一阶非齐次线性微分方程。

为了求解方程(6)的通解，我们先求它所对应的齐次线性微分方程 $$\frac{dy}{dx}+P(x)y=0\tag{7}$$ 的通解。因为方程(7)是可分离变量的方程，分离变量得 $$\frac{dy}{y}=-P(x)dx$$ 两端积分得 $$ln|y|=-\int{P(x)dx}+ln|C|$$ 整理得 $$y=Ce^{-\int{P(x)dx}}$$ 其中，C为任意常数，这是对应齐次线性微分方程(7)的通解。

为了求解非齐次线性微分方程(6)的解，我们从齐次线性微分方程(7)的通解出发，将齐次线性微分方程(7)的通解中的任意常数C变为x的一个待定函数 C(x) ，如果能找到 C(x)，使得 $$y=C(x)e^{-\int{P(x)dx}}\tag{8}$$ 满足非齐次线性微分方程(6)，则函数(8)就是非齐次性线微分方程(6)的通解。为此，将方程(8)代入非齐次线性微分方程(6)，有 $$C'(x)e^{-\int{P(x)dx}}-P(x)C(x)e^{-\int{P(x)dx}}+P(x)C(x)e^{-\int{P(x)dx}}=Q(x)$$ 整理得 $$C'(x)=Q(x)e^{\int{P(x)dx}}$$ 两端积分得 $$C(x)=\int{Q(x)e^{\int{P(x)dx}}}+C$$ 故一阶非齐次线性微分方程(6)的通解为 $$y=e^{-\int{P(x)dx}}\left[\int{Q(x)e^{\int{P(x)dx}}}+C\right]$$ 或 $$y=Ce^{-\int{P(x)dx}}+e^{-\int{P(x)dx}} \int{Q(x)e^{\int{P(x)dx}}}dx$$ 式中第一项是对应齐次线性微分方程(7)的通解，第二项是非齐次线性微分方程(6)的一个特解。由此可知，一阶非齐次线性微分方程的通解等于对应的齐次线性微分方程的通解与非齐次线性微分方程的一个特解之和。

这种方法称为常数变易法。其计算步骤为：
(1) 求出对应齐次线性微分方程(7)的通解；
(2) 将齐次线性微分方程(7)的通解中的常数C变成待定的函数C(x)得到方程(8)，并设方程(8)是非齐次线性微分方程(6)的通解；
(3) 将方程(8)代入非齐次线性微分方程(6)，求出待定函数C(x)；
(4) 将求出的C(x)代入(8)，就得到非齐次线性微分方程(6)的通解。

例 5 求微分方程 $$(x+1)\frac{dy}{dx}-ny=(x+1)^{n+1}e^x$$ 的通解。

解所求方程为一阶非齐次线性微分方程，将方程改写为 $$\frac{dy}{dx}-\frac{n}{x+1}y=(x+1)^ne^x$$ 其对应的齐次线性微分方程为 $$\frac{dy}{dx}-\frac{n}{x+1}y=0$$ 分离变量得 $$\frac{dy}{y}=\frac{ndx}{x+1}$$ 两端积分得 $$ln|y|=nln|x+1|+ln|C|$$ 故对应齐次线性微分方程的通解为 $$y=C(x+1)^n$$ 其中，C是任意常数。
下面利用常数变易法求非齐次线性微分方程的通解。设原方程的通解为 $$y=C(x)(x+1)^n$$ 代入原方程，可得 $$C'(x)(x+1)^n+nC(x)(x+1)^{n-1}-\frac{n}{x+1}C(x)(x+1)^n=(x+1)^ne^x$$ 整理得 $$C'(x)=e^x$$ 两端积分得 $$C(x)=e^x+C$$ 故所求微分方程的通解为 $$y=C(x+1)^n+(x+1)^ne^x$$ 其中，C是任意常数。

例 6 求微分方程 $$cosx\frac{dy}{dx}+ysinx=1$$ 的通解。

解将方程改写为 $$\frac{dy}{dx}+ytanx=secx$$ 此方程为线性微分方程，利用一阶非齐次线性微分方程的通解公式，所求方程的通解为 $$ \begin{aligned} y&=Ce^{-\int{tanxdx}}+e^{-\int{tanxdx}}\int{secxe^{\int{tanxdx}}dx}\\ &=Ccosx+cosx\int{secx\frac{1}{cosx}dx}\\ &=Ccosx+cosxtanx\\ &=Ccosx+sinx \end{aligned} $$ 其中，C是任意常数。

例 7 求微分方程$\frac{dy}{dx}-\frac{y}{x}=-\frac{6x^2+1}{x}$满足$y(1)=0$的特解。

解由于方程是一阶线性微分方程，对应的齐次方程为 $$\frac{dy}{dx}-\frac{y}{x}=0$$ 分离变量得 $$\frac{dy}{y}=\frac{dx}{x}$$ 两端积分得 $$ln|y|=ln|x|+ln|C|$$ 故对应齐次线性微分方程的通解为 $$y=Cx$$ 其中，C是任意常数。
下面利用常数变易法求非齐次线性微分方程的通解。设原方程的通解为 $$y=C(x)x$$ 代入原方程，可得 $$C'(x)x+C(x)-\frac{C(x)x}{x}=-\frac{6x^2+1}{x}$$ 整理得 $$C'(x)=-\frac{6x^2+1}{x^2}=-6-\frac{1}{x^2}$$ 两端积分得 $$C(x)=-6x+\frac{1}{x}+C$$ 故所求微分方程的通解为 $$y=Cx-6x^2+1$$ 其中，C是任意常数。
又因为当x=1时，有y=0，代入上式得C=5，故所求方程的特解为 $$y=5x-6x^2+1$$

例 8 求微分方程 $$\frac{dy}{dx}=\frac{y}{2x+y^3}$$ 的通解。

解所求方程不是未知函数y的线性方程。但是，将x看成y的函数时，得 $$\frac{dx}{dy}-\frac{2}{y}x=y^2$$ 这是关于未知函数x的线性方程，y为自变量。其对应的齐次线性微分方程 $$\frac{dx}{dy}-\frac{2x}{y}=0$$ 的通解为 $$x=Cy^2$$ 利用常数变易法，令$x=C(y)y^2$，代入非齐次线性微分方程，可得 $$C'(y)y^2=y^2$$ 整理得 $$C'(y)=1$$ 两端积分得 $$C(y)=y+C$$ 故所求方程的通解为 $$x=Cy^2+y^3$$ 其中，C是任意常数。

标签: Algorithms