鸟语天空

三角形重心坐标空间

作者：追风剑情 发布于：2023-11-29 10:48 分类：Algorithms

  虽然我们经常在 3D 中使用三角形，但三角形的表面是一个平面，它天生是一个 2D 物体。在 3D 中任意朝向的三角形表面上移动是一件令人烦恼的事。最好是有一个坐标空间与三角形表面相关联且独立于三角形所在的 3D 坐标空间。重心坐标空间正是这样的坐标空间。

  三角形所在平面的任意点都能表示为顶点的加权平均值。这个权就称作重心坐标,从重心坐标(b₁, b₂, b₃)到标准3D坐标的转换为: \begin{flalign} &(b_1,b_2,b_3)\Leftrightarrow b_1 \mathbf{v}_1 + b_2 \mathbf{v}_2 + b_3 \mathbf{v}_3 \tag{公式 12.21 从重心坐标中计算 3D 点坐标}&\\ \end{flalign}

重心坐标的总合是 1: \begin{flalign} &b_1 + b_2 + b_3 = 1 &\\ \end{flalign}

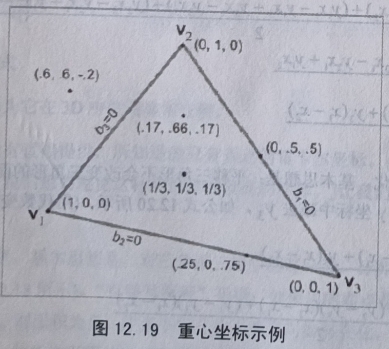
b₁，b₂和b₃的值是每个顶点对该点的“贡献”或“权”。下图展示了一些点和它们的重心坐标。

这里应注意以下几点：

• 第一。三角形三个顶点的重心坐标都是单位向量: \begin{flalign} &(1,0,0) \Leftrightarrow \mathbf{v}_1 &\\ &(0,1,0) \Leftrightarrow \mathbf{v}_2 &\\ &(0,0,1) \Leftrightarrow \mathbf{v}_3 &\\ \end{flalign}
• 第二。在某顶点的相对边上的所有点的对应重心坐标分量为0。例如，对于所有与v₁相对边上的点，b₁=0。
• 第三。不只是三角形内的点，该平面上的所有点都能用重心坐标描述。三角形内的点的重心坐标在范围 0 到 1 之间变化。三角形外的点至少有一个坐标为负。重心坐标用和原三角形大小相同的块“嵌满”整个平面。如图 12.20 所示。
  

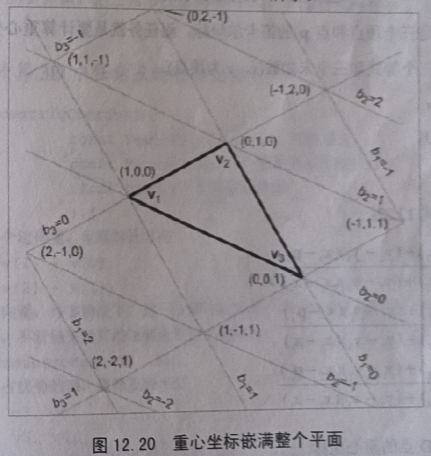
  重心坐标空间的本质不同于笛卡尔坐标空间。这是因为重心坐空间系是 2D 的，但却使用了三个坐标。又因为坐标的和等于 1，所以重心坐标空间仅有两个自由度，有一个分量是冗余的。从另一方面说，重心坐标空间中仅用两个数就能完全的描述一个点，用这两个数就可以计算出第三个。

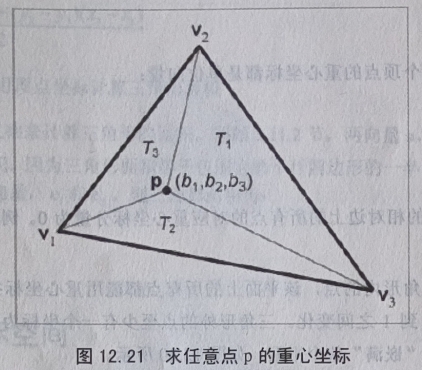
  要将一个点从重心坐标空间转换到普通的 3D 坐标空间，只需要应用公式 12.21 来计算顶点加权平值就可以了。而计算 2D 或 3D 中任意一点的重心坐标就稍微困难一些。让我们看看怎样在 2D 中做到这一点。见图 12.21，它标出了三个顶点v₁，v₂，v₃和点p。我们还标出了三个“子三角形”T₁，T₂，T₃，它们和同样下标的顶点相对。稍后会用到它们。

  现在，我们知道的是三个顶点和点 p 的笛卡尔坐标，而任务就是要计算重心坐标b₁，b₂和b₃。根据这些已知条件可以列出三个等式和三个未知数(x，y为顶点) \begin{flalign} &\mathbf{p}_x=b_1 x_1 + b_2 x_2 + b_3 x_3 &\\ &\mathbf{p}_y=b_1 y_1 + b_2 y_2 + b_3 y_3 &\\ &b_1 + b_2 + b_3 = 1 &\\ \end{flalign} 解这个方程组得公式: \begin{flalign} &b_1=\frac{(\mathbf{p}_y - y_3)(x_2 - x_3)+(y_2 - y_3)(x_3-\mathbf{p}_x)}{(y_1 - y_3)(x_2 - x_3)+(y_2 - y_3)(x_3 - x_1)} &\\ &b_2=\frac{(\mathbf{p}_y-y_1)(x_3-x_1)+(y_3-y_1)(x_1-\mathbf{p}_x)}{(y_1 - y_3)(x_2 - x_3)+(y_2 - y_3)(x_3 - x_1)} \tag{公式 12.22 求 2D 点的重心坐标}&\\ &b_3=\frac{(\mathbf{p}_y-y_2)(x_1-x_2)+(y_1-y_2)(x_2-\mathbf{p}_x)}{(y_1 - y_3)(x_2 - x_3)+(y_2 - y_3)(x_3 - x_1)} &\\ \end{flalign}

仔细观察公式 12.22，发现每个表达式中的分母相同，并且都等于三角形面积的两倍 (参见 已知三角形各顶点的笛卡尔坐标求面积公式) 还有，对每个重心坐标b，其分子等于“子三角形”T面积的两倍。换句话说: \begin{flalign} &b_1=A(T_1)/A(T) &\\ &b_2=A(T_2)/A(T) \tag{公式 12.23 把重心坐标解释成面积比}&\\ &b_3=A(T_3)/A(T) &\\ \end{flalign}

  注意，即使 p 在三角形外，这个解释也是成立的，这是因为如果顶点以逆时针方向列出，计算面积的公式将得到一个负值。如果三角形的三个顶点共线，分母上的“子三角形”的面积为零，重心坐标也就没有定义。

  计算 3D 中任意点的重心坐标比在 2D 中复杂。不能再像以前那样解一个方程组了，因为有三个未知数和四个方程。另一个导致复杂性的地方是p可能不在三角形所在的平面中，这时重心坐标没有意义。但现在我们假设 p 在三角形所在的平面上。

  一种技巧是通过抛弃x，y，z之中的一个分量，将 3D 问题转化到 2D 中，这和将三角形投影到三个基本平面中的某一个上面的原理相同。理论上，这是能解决问题的，因为投影面积和原面积成比例。

  那么应该抛弃哪个坐标呢？不能总是抛弃某一个，因为如果三角形垂直于某个平面，投影点将共线如果三角形接近垂直于投影平面，会遇到浮点数精度问题。一种解决方法是挑选投影平面，使得投影面积最大。这可以通过检查平面的法向量做到，我们要抛弃的就是绝对值最大的坐标。例如，法向量为[-1，0，0]。我们将抛弃顶点和 p 的 x 分量，把三角形投影到 yz 平面。下面的代码展示了怎样计算 3D 中任意点的重心坐标:

using System;
public class Program
{
    static void Main(string[] args)
    {
        Vector3 v1 = new Vector3(1, 0, 0);
        Vector3 v2 = new Vector3(0, 0, 1);
        Vector3 v3 = new Vector3(1, 1, 1);
        Vector3[] v = { v1, v2, v3 };
        Vector3 p = new Vector3(0.5f, 0.5f, 0.5f);
        Vector3 b;
        ComputeBarycentricCoords3d(v, p, out b);
        Console.WriteLine("b=({0},{1},{2})", b.x, b.y, b.z);
        Console.ReadKey();
    }

    /// <summary>
    /// 计算p点的重心空间坐标
    /// </summary>
    /// <param name="v">三角形各顶点坐标</param>
    /// <param name="p">要计算的坐标</param>
    /// <param name="b">p点对应的重心坐标</param>
    /// <returns></returns>
    public static bool ComputeBarycentricCoords3d(Vector3[] v, Vector3 p, out Vector3 b)
    {
        b.x = b.y = b.z = 0;
        //首先，计算两个边向量，呈顺时针方向
        Vector3 d1 = v[1] - v[0];
        Vector3 d2 = v[2] - v[1];
        //用叉乘计算法向量，许多情况下，这一步都可以省路，因为法向量是预先计算的
        //不需要正则化，不管预先计算的法向量是否正则化过。
        Vector3 n = Vector3.CrossProduct(d1, d2);
        //判断法向量中占优势的轴，选择投影平面
        float u1, u2, u3, u4;
        float v1, v2, v3, v4;
        if (Math.Abs(n.x) >= Math.Abs(n.y) && Math.Abs(n.x) >= Math.Abs(n.z))
        {
            Console.WriteLine("yz平面投影");
            //抛弃x，向yz平面投影
            u1 = v[0].y - v[2].y;
            u2 = v[1].y - v[2].y;
            u3 = p.y - v[0].y;
            u4 = p.y - v[2].y;
            v1 = v[0].z - v[2].z;
            v2 = v[1].z - v[2].z;
            v3 = p.z - v[0].z;
            v4 = p.z - v[2].z;
        }
        else if (Math.Abs(n.y) >= Math.Abs(n.z))
        {
            Console.WriteLine("xz平面投影");
            //抛弃y，向xz平面投影
            u1 = v[0].z - v[2].z;
            u2 = v[1].z - v[2].z;
            u3 = p.z - v[0].z;
            u4 = p.z - v[2].z;
            v1 = v[0].x - v[2].x;
            v2 = v[1].x - v[2].x;
            v3 = p.x - v[0].x;
            v4 = p.x - v[2].x;
        }
        else
        {
            Console.WriteLine("xy平面投影");
            //抛弃z，向xy平面投影
            u1 = v[0].x - v[2].x;
            u2 = v[1].x - v[2].x;
            u3 = p.x - v[0].x;
            u4 = p.x - v[2].x;
            v1 = v[0].y - v[2].y;
            v2 = v[1].y - v[2].y;
            v3 = p.y - v[0].y;
            v4 = p.y - v[2].y;
        }
        //计算分母，并判断是否合法
        float denom = v1 * u2 - v2 * u1;
        if (denom == 0.0f)
        {
            //退化三角形--面积为零的三角形
            return false;
        }
        //计算重心坐标
        float oneOverDenom = 1.0f / denom;
        b.x = (v4 * u2 - v2 * u4) * oneOverDenom;
        b.y = (v1 * u3 - v3 * u1) * oneOverDenom;
        b.z = 1.0f - b.x - b.y;
        return true;
    }

    public struct Vector3
    {
        public float x;
        public float y;
        public float z;

        public Vector3(float x, float y, float z)
        {
            this.x = x;
            this.y = y;
            this.z = z;
        }

        public static Vector3 operator -(Vector3 l, Vector3 r)
        {
            Vector3 v;
            v.x = l.x - r.x;
            v.y = l.y - r.y;
            v.z = l.z - r.z;
            return v;
        }

        public static Vector3 operator *(Vector3 l, Vector3 r)
        {
            Vector3 v;
            v.x = l.x * r.x;
            v.y = l.y * r.y;
            v.z = l.z * r.z;
            return v;
        }

        public static Vector3 CrossProduct(Vector3 l, Vector3 r)
        {
            Vector3 v;
            v.x = l.y * r.z - r.y * l.z;
            v.y = l.z * r.x - r.z * l.x;
            v.z = l.x * r.y - r.x * l.y;
            return v;
        }
    }
}

标签: Algorithms