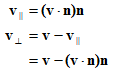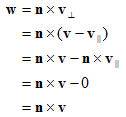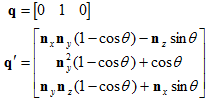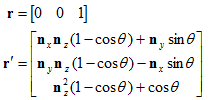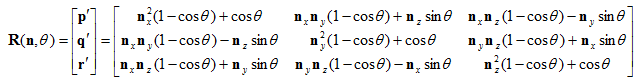3D中绕任意轴的旋转
作者:追风剑情 发布于:2018-7-13 21:08 分类:计算机图形学
这里讨论绕通过原点的任意轴。用单位向量n描述旋转轴,用θ描述旋转量。
让我们导出绕轴n旋转角度θ的矩阵。也就是说,我们想得到满足下面条件的矩阵
vR(n, θ)=v'
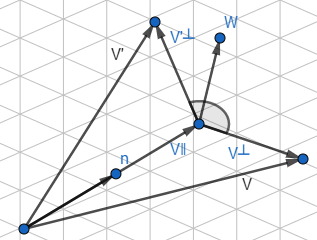
v'是向量v绕轴n旋转后的向量。让我们看看能否用v,n和θ表示v'。我们的想法是在垂直于n的平面中解决这个问题,那么这就转换为了一个简单的2D问题。为了做到这一点,将v分解为两个分量:v∥和v⊥,分别平行于n和垂直于n,并有v=v∥+v⊥。因为v∥平行于n,所以绕n旋转不会影响它。故只要计算出v⊥绕n旋转后的v⊥',就能得到v'=v∥+v⊥',我们构造向量v∥,v⊥和临时向量w,如图所示。
上图展示了以下向量:
- v∥是v平行于n的分量。另一种说法就是v∥是v在n上的投影,用(v●n)n计算。
- v⊥是v垂直于n的分量。因为v=v∥+v⊥,所以v⊥=v-v∥。v⊥是v投影到垂直于n的平面上的结果。
- w是同时垂直于v∥和v⊥的向量。它的长度和v⊥的相同。w和v⊥同在垂直于n的平面中。w是v⊥绕n旋转90度的结果,由n×v⊥可以得到。
现在,v'垂直于n的分量可以表示为:
代换v⊥和w:
代入v'的表达式,有:
现在,已经得到v'与v,n,θ的关系公式了,可以用它来计算变换后的基向量并构造矩阵。第一个基向量为:
另外两个基向量的推导与之类似,有:
注意:上面我们只使用了列向量,这样做的目的是使等式整洁清晰、易于理解。
用这些基向量构造矩阵,可得公式为:
标签: 计算机图形学
日历
最新文章
随机文章
热门文章
分类
存档
- 2026年1月(5)
- 2025年12月(1)
- 2025年11月(1)
- 2025年9月(3)
- 2025年7月(4)
- 2025年6月(5)
- 2025年5月(1)
- 2025年4月(5)
- 2025年3月(4)
- 2025年2月(3)
- 2025年1月(1)
- 2024年12月(5)
- 2024年11月(5)
- 2024年10月(5)
- 2024年9月(3)
- 2024年8月(3)
- 2024年7月(11)
- 2024年6月(3)
- 2024年5月(9)
- 2024年4月(10)
- 2024年3月(11)
- 2024年2月(24)
- 2024年1月(12)
- 2023年12月(3)
- 2023年11月(9)
- 2023年10月(7)
- 2023年9月(2)
- 2023年8月(7)
- 2023年7月(9)
- 2023年6月(6)
- 2023年5月(7)
- 2023年4月(11)
- 2023年3月(6)
- 2023年2月(11)
- 2023年1月(8)
- 2022年12月(2)
- 2022年11月(4)
- 2022年10月(10)
- 2022年9月(2)
- 2022年8月(13)
- 2022年7月(7)
- 2022年6月(11)
- 2022年5月(18)
- 2022年4月(29)
- 2022年3月(5)
- 2022年2月(6)
- 2022年1月(8)
- 2021年12月(5)
- 2021年11月(3)
- 2021年10月(4)
- 2021年9月(9)
- 2021年8月(14)
- 2021年7月(8)
- 2021年6月(5)
- 2021年5月(2)
- 2021年4月(3)
- 2021年3月(7)
- 2021年2月(2)
- 2021年1月(8)
- 2020年12月(7)
- 2020年11月(2)
- 2020年10月(6)
- 2020年9月(9)
- 2020年8月(10)
- 2020年7月(9)
- 2020年6月(18)
- 2020年5月(4)
- 2020年4月(25)
- 2020年3月(38)
- 2020年1月(21)
- 2019年12月(13)
- 2019年11月(29)
- 2019年10月(44)
- 2019年9月(17)
- 2019年8月(18)
- 2019年7月(25)
- 2019年6月(25)
- 2019年5月(17)
- 2019年4月(10)
- 2019年3月(36)
- 2019年2月(35)
- 2019年1月(28)
- 2018年12月(30)
- 2018年11月(22)
- 2018年10月(4)
- 2018年9月(7)
- 2018年8月(13)
- 2018年7月(13)
- 2018年6月(6)
- 2018年5月(5)
- 2018年4月(13)
- 2018年3月(5)
- 2018年2月(3)
- 2018年1月(8)
- 2017年12月(35)
- 2017年11月(17)
- 2017年10月(16)
- 2017年9月(17)
- 2017年8月(20)
- 2017年7月(34)
- 2017年6月(17)
- 2017年5月(15)
- 2017年4月(32)
- 2017年3月(8)
- 2017年2月(2)
- 2017年1月(5)
- 2016年12月(14)
- 2016年11月(26)
- 2016年10月(12)
- 2016年9月(25)
- 2016年8月(32)
- 2016年7月(14)
- 2016年6月(21)
- 2016年5月(17)
- 2016年4月(13)
- 2016年3月(8)
- 2016年2月(8)
- 2016年1月(18)
- 2015年12月(13)
- 2015年11月(15)
- 2015年10月(12)
- 2015年9月(18)
- 2015年8月(21)
- 2015年7月(35)
- 2015年6月(13)
- 2015年5月(9)
- 2015年4月(4)
- 2015年3月(5)
- 2015年2月(4)
- 2015年1月(13)
- 2014年12月(7)
- 2014年11月(5)
- 2014年10月(4)
- 2014年9月(8)
- 2014年8月(16)
- 2014年7月(26)
- 2014年6月(22)
- 2014年5月(28)
- 2014年4月(15)
友情链接
- Unity官网
- Unity圣典
- Unity在线手册
- Unity中文手册(圣典)
- Unity官方中文论坛
- Unity游戏蛮牛用户文档
- Unity下载存档
- Unity引擎源码下载
- Unity服务
- Unity Ads
- wiki.unity3d
- Visual Studio Code官网
- SenseAR开发文档
- MSDN
- C# 参考
- C# 编程指南
- .NET Framework类库
- .NET 文档
- .NET 开发
- WPF官方文档
- uLua
- xLua
- SharpZipLib
- Protobuf-net
- Protobuf.js
- OpenSSL
- OPEN CASCADE
- JSON
- MessagePack
- C在线工具
- 游戏蛮牛
- GreenVPN
- 聚合数据
- 热云
- 融云
- 腾讯云
- 腾讯开放平台
- 腾讯游戏服务
- 腾讯游戏开发者平台
- 腾讯课堂
- 微信开放平台
- 腾讯实时音视频
- 腾讯即时通信IM
- 微信公众平台技术文档
- 白鹭引擎官网
- 白鹭引擎开放平台
- 白鹭引擎开发文档
- FairyGUI编辑器
- PureMVC-TypeScript
- 讯飞开放平台
- 亲加通讯云
- Cygwin
- Mono开发者联盟
- Scut游戏服务器引擎
- KBEngine游戏服务器引擎
- Photon游戏服务器引擎
- 码云
- SharpSvn
- 腾讯bugly
- 4399原创平台
- 开源中国
- Firebase
- Firebase-Admob-Unity
- google-services-unity
- Firebase SDK for Unity
- Google-Firebase-SDK
- AppsFlyer SDK
- android-repository
- CQASO
- Facebook开发者平台
- gradle下载
- GradleBuildTool下载
- Android Developers
- Google中国开发者
- AndroidDevTools
- Android社区
- Android开发工具
- Google Play Games Services
- Google商店
- Google APIs for Android
- 金钱豹VPN
- TouchSense SDK
- MakeHuman
- Online RSA Key Converter
- Windows UWP应用
- Visual Studio For Unity
- Open CASCADE Technology
- 慕课网
- 阿里云服务器ECS
- 在线免费文字转语音系统
- AI Studio
- 网云穿
- 百度网盘开放平台
- 迅捷画图
- 菜鸟工具
- [CSDN] 程序员研修院
- 华为人脸识别
- 百度AR导航导览SDK
- 海康威视官网
- 海康开放平台
- 海康SDK下载
- git download
- Open CASCADE
- CascadeStudio
交流QQ群
-
Flash游戏设计: 86184192
Unity游戏设计: 171855449
游戏设计订阅号