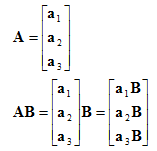因为矩阵乘法满足结合律，可以先把所有变换矩阵组合起来，这样向量只需乘以一个最终变换矩阵。

矩阵组合从代数角度看是利用了矩阵乘法的结合律。

从几何角度看，矩阵的行向量就是变换后的基向量。这在多个变换的情况下也是成立的。参见 矩阵几何解释

考虑矩阵乘法AB，结果中的每一行都是A中相应行与矩阵B相乘的结果。换言之，设a1,a2,a3为A的行，矩阵乘法能够写为：

这使得结论更加清晰，AB结果中的行向量确实是对A的基向量进行B变换的结果。