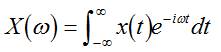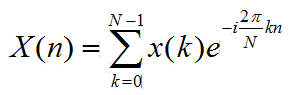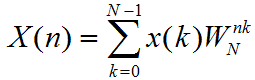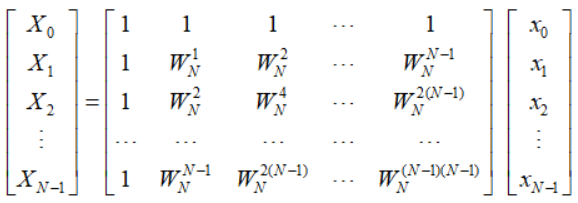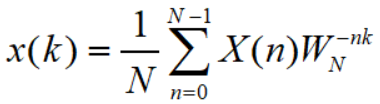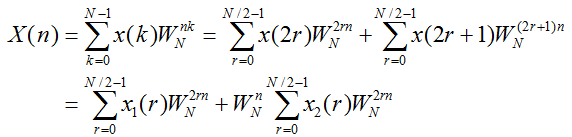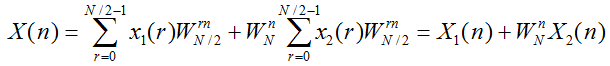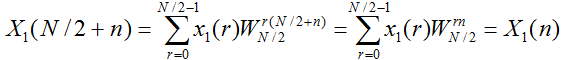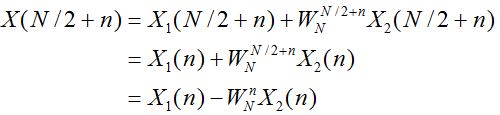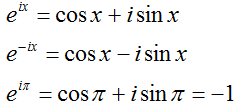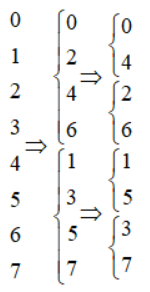快速傅里叶算法(FFT)示例
post by:追风剑情 2018-2-23 18:25
连续非周期信号的傅里叶变换公式
(公式中的i是虚数单位)
现在假设在x(t)的某一段连续区间上以周期T进行采样，得到N个采样点，则每个采样点的离散傅里叶变换公式就是：
(n=0,1,...,N-1)
令
,则上式可简单记为:
(n=0,1,...,N-1)
上式可用线性方程组表示为:
for (int n=0; n<N; n++) for (int k=0; k<N; k++) int p = n * k;//旋转因子指数
逆变换公式
被称为旋转因子。
的周期性可以表示为
的对称性可以表示为
的可约性可以表示为
原始信号与两个分组信号之间的关系:
每次分解，都将原始信号x(n)按照时间顺序(也就是n的序号)分成奇、偶两个组x1(r)和x2(r)，其中r与n的关系是:
当n为偶数时，令n=2r;
当n为奇数时，令n=2r+1;
也就是说，原始信号与两个分组的信号存在以下关系:
x(2r)=x1(r), x(2r+1)=x2(r) 其中r=0,1,...,N/2-1
将一个N点DFT分解为两个N/2点DFT：
因为
，代入上式，得到：
由周期性可知:
,因此：
同理可得：
由以上关系可知：
一个N点DFT变换的前N/2个周期数据的转换关系是:
(n=0,1,...,N/2-1)
一个N点DFT变换的后N/2个周期数据的转换关系是:
(n=0,1,...,N/2-1)
欧拉公式
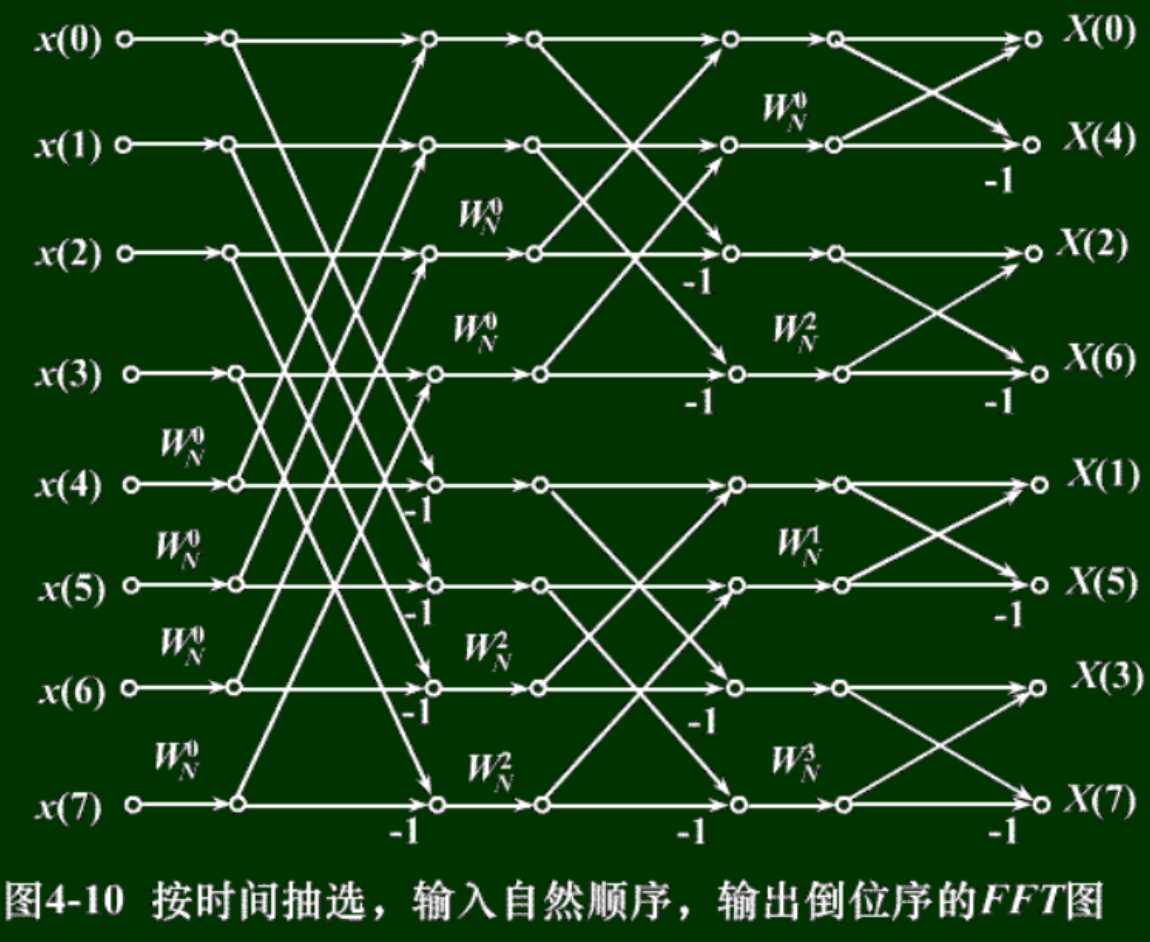
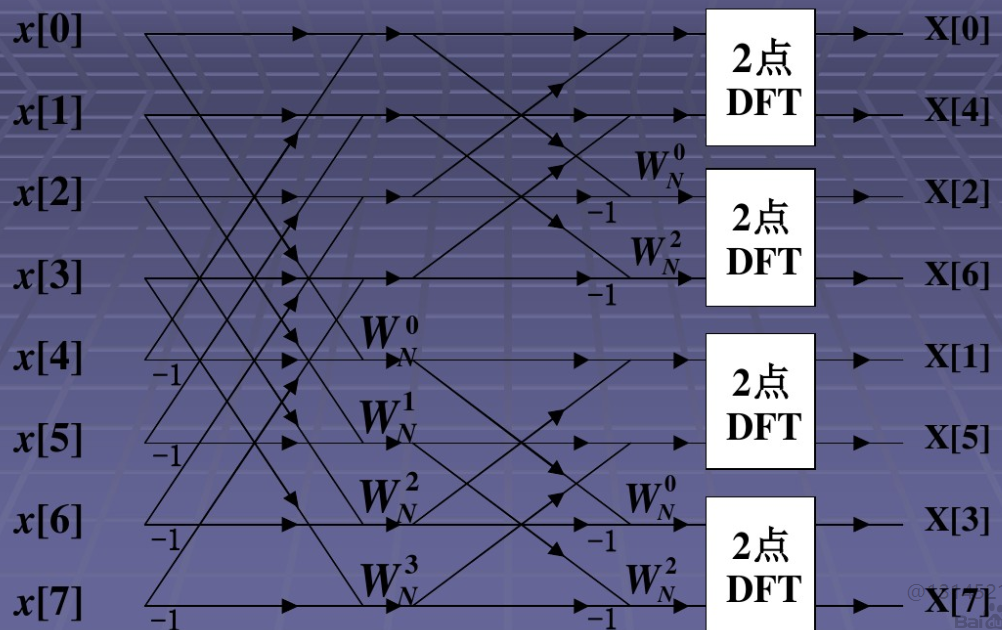
从上面的公式可知，FFT是递归求解过程。不断对数据进行奇偶分组，如下图:
蝶形算法流程图(借用网上一张截图)
旋转因子WNP规律
P = i*(1<<L); (i为第几次蝶形运算, L为当前级数(从0开始算))
FFT算法的复量运算量为
图像处理：先进行行变换，再对变换结果进行列变换，或者先进行列变换，再对结果进行行变换。
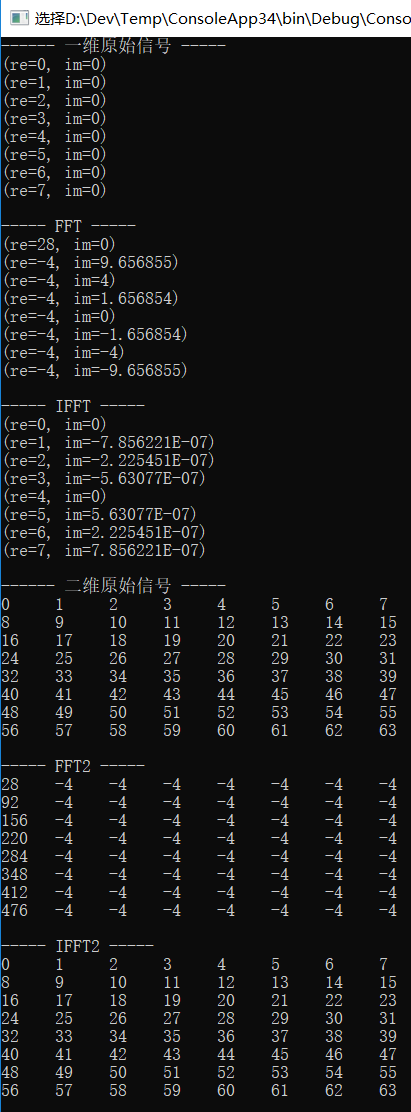
示例
using System;
using System.Collections.Generic;
namespace ConsoleApp34
{
class Program
{
static void Main(string[] args)
{
TestFFT();
TestFFT2();
Console.Read();
}
private static void TestFFT()
{
const int N = 8;
//初始化时域数据
Complex[] TD2FD = new Complex[N];
for (int i = 0; i < N; i++)
{
Complex cpx = new Complex();
cpx.re = i;
cpx.im = 0;
TD2FD[i] = cpx;
}
Console.WriteLine("------ 一维原始信号 -----");
Print(TD2FD);
Console.WriteLine("----- FFT -----");
FFT(TD2FD);
Print(TD2FD);
Console.WriteLine("----- IFFT -----");
IFFT(TD2FD);
Print(TD2FD);
}
private static void TestFFT2()
{
const int W = 8, H = 8;
Complex2D complex2D = new Complex2D(W, H);
for (int i=0; i<H; i++)
{
for (int j=0; j<W; j++)
{
Complex cpx = new Complex();
cpx.re = i * W + j;
cpx.im = 0;
complex2D.SetComplex(i, j, cpx);
}
}
Console.WriteLine("------ 二维原始信号 -----");
complex2D.Print();
Console.WriteLine("----- FFT2 -----");
FFT2(complex2D);
complex2D.Print();
Console.WriteLine("----- IFFT2 -----");
IFFT2(complex2D);
complex2D.Print();
}
//快速傅里叶变换
public static void FFT(Complex[] TD2FD)
{
FFT_Core(TD2FD, WT_LUT(TD2FD.Length, 1));
}
//快速傅里叶变换 (二维)
public static void FFT2(Complex2D TD2FD)
{
//对每一行做FFT
for (int i=0; i<TD2FD.Height; i++)
{
Complex[] row = TD2FD.GetRow(i);
FFT(row);
}
//对每一列做FFT
for (int i = 0; i < TD2FD.Width; i++)
{
Complex[] column = TD2FD.GetColumn(i);
FFT(column);
}
}
//快速傅里叶逆变换
public static void IFFT(Complex[] FD2TD)
{
//做FFT变换
Complex[] WT = WT_LUT(FD2TD.Length, -1);
FFT_Core(FD2TD, WT);
//除以N
for (int i = 0; i < FD2TD.Length; i++) {
FD2TD[i].re /= FD2TD.Length;
FD2TD[i].im /= FD2TD.Length;
}
}
//快速傅里叶逆变换 (二维)
public static void IFFT2(Complex2D FD2TD)
{
//对每一行做IFFT
for (int i = 0; i < FD2TD.Height; i++)
{
Complex[] row = FD2TD.GetRow(i);
IFFT(row);
}
//对每一列做IFFT
for (int i = 0; i < FD2TD.Width; i++)
{
Complex[] column = FD2TD.GetColumn(i);
IFFT(column);
}
}
// 返回旋转因子查询表(twiddle factor lookup table)
private static Complex[] WT_LUT(int N, int flag = 1)
{
Complex[] WT = new Complex[N];
for (int i = 0; i < N; i++)
{
Complex cpx_wt = new Complex();
float angle = (float)(-i * Math.PI * 2 / N);
cpx_wt.re = (float)Math.Cos(angle);
//IFFT flag=-1, FFT flag=1
cpx_wt.im = flag * (float)Math.Sin(angle);
WT[i] = cpx_wt;
}
return WT;
}
private static void FFT_Core(Complex[] TD2FD, Complex[] WT)
{
int power = (int)Math.Log(TD2FD.Length, 2);
int butterfly;
int p, s;
Complex x1, x2, wt;
//倒位排序
BitReverse(TD2FD);
//蝶形运算
for (int k = 0; k < power; k++) //级数
{
for (int j = 0; j < 1 << (power - k - 1); j++) //组数
{
//每组有几个元素
butterfly = 1 << k + 1;
//计算参与蝶形运算的两个元素的索引
p = j * butterfly;
s = p + butterfly / 2;
for (int i = 0; i < butterfly / 2; i++) //蝶形运算次数
{
x1 = TD2FD[i + p];
x2 = TD2FD[i + s];
wt = WT[i * TD2FD.Length / butterfly];
TD2FD[i + p] = x1 + x2 * wt;
TD2FD[i + s] = x1 - x2 * wt;
}
}
}
}
private static int BitReverse(int x)
{
//倒位排序
//0 1 2 3 4 5 6 7 十进制
//000 001 010 011 100 101 110 111 十进制对应的二进制
//000 100 010 110 001 101 011 111 码位反转
//0 4 2 6 1 5 3 7 码位反转后对应的十进制
int[] table = new int[8] { 0, 4, 2, 6, 1, 5, 3, 7 };
return table[x];
}
// 倒位排序——雷德算法
private static void BitReverse(Complex[] array)
{
int i, j, k;
int N = array.Length;
Complex temp;
j = 0;
for (i = 0; i < N - 1; i++)
{
if (i < j)
{
temp = array[i];
array[i] = array[j];
array[j] = temp;
}
// 求j的下一个倒序位
// N/2的二进制最高位为1，其他位都为0
// 判断最高位是否为1，可与N/2进行比较
// 判断次高位是否为1，可与N/4进行比较
k = N >> 1;
//如果k<=j,表示j的最高位为1
while (k <= j)
{
//当k<=j时，需要将最高位变为0
j = j - k;
//判断次高位是否为1,依次类推，逐个比较，直到j某个位为0
k >>= 1;
}
j = j + k;//将0变为1
}
}
// 打印
private static void Print(Complex[] TD2FD)
{
for (int i = 0; i < TD2FD.Length; i++)
{
Console.WriteLine("(re={0}, im={1})", TD2FD[i].re, TD2FD[i].im);
}
Console.WriteLine();
}
}
//定义复数
public class Complex
{
public float re;//实数部
public float im;//虚数部
// 幅值
public double Amplitude
{
get {
return Math.Sqrt(re*re + im*im);
}
}
// 相位
public double Phase
{
get {
return Math.Atan2(im, re);
}
}
public static Complex operator +(Complex lhs, Complex rhs)
{
Complex result = new Complex();
result.re = lhs.re + rhs.re;
result.im = lhs.im + rhs.im;
return result;
}
public static Complex operator -(Complex lhs, Complex rhs)
{
Complex result = new Complex();
result.re = lhs.re - rhs.re;
result.im = lhs.im - rhs.im;
return result;
}
public static Complex operator *(Complex lhs, Complex rhs)
{
Complex result = new Complex();
result.re = lhs.re * rhs.re - lhs.im * rhs.im;
result.im = lhs.re * rhs.im + lhs.im * rhs.re;
return result;
}
public static Complex operator *(float lhs, Complex rhs)
{
Complex result = new Complex();
result.re = lhs * rhs.re;
result.im = lhs * rhs.im;
return result;
}
public static Complex operator *(Complex lhs, float rhs)
{
Complex result = new Complex();
result.re = lhs.re * rhs;
result.im = lhs.im * rhs;
return result;
}
}
public class Complex2D
{
private List<Complex[]> rows = new List<Complex[]>();
private List<Complex[]> columns = new List<Complex[]>();
private int m_width;
private int m_height;
public Complex2D(int width, int height)
{
m_width = width;
m_height = height;
for (int i = 0; i < height; i++)
rows.Add(new Complex[width]);
for (int i = 0; i < width; i++)
columns.Add(new Complex[height]);
}
public int Width { get { return m_width; } }
public int Height { get { return m_height; } }
public Complex[] GetRow(int i)
{
return rows[i];
}
public Complex[] GetColumn(int i)
{
return columns[i];
}
public void SetRow(int i, Complex[] src)
{
rows[i] = src;
}
public void SetColumn(int i, Complex[] src)
{
columns[i] = src;
}
public void SetComplex(int i, int j, Complex src)
{
rows[i][j] = src;
columns[j][i] = src;
}
public void SetComplexs(Complex[][] src)
{
for (int i=0; i<src.Length; i++)
{
Complex[] row = src[i];
for (int j = 0; j < row.Length; j++)
SetComplex(i, j, row[j]);
}
}
public void Print()
{
for (int i=0; i<rows.Count; i++)
{
Complex[] row = rows[i];
for (int j = 0; j < row.Length; j++)
Console.Write("{0:G} ", row[j].re.ToString().PadRight(5));
Console.WriteLine();
}
Console.WriteLine();
}
}
}
运行测试
//频谱分析窗函数类型
public enum FFTWindow
{
//
// 矩形窗 (使用最多的窗)
// W[n] = 1.0.
Rectangular = 0,
//
// 三角窗
// W[n] = TRI(2n/N).
Triangle = 1,
//
// 汉宁窗(余弦窗)
// W[n] = 0.54 - (0.46 * COS(n/N) ).
Hamming = 2,
//
// 海明窗(升余弦窗)
// W[n] = 0.5 * (1.0 - COS(n/N) ).
Hanning = 3,
//
// 布拉克曼
// W[n] = 0.42 - (0.5 * COS(nN) ) + (0.08 * COS(2.0 * nN) ).
Blackman = 4,
//
// 哈布斯窗
// W[n] = 0.35875 - (0.48829 * COS(1.0 * nN)) + (0.14128 * COS(2.0 * nN)) - (0.01168 * COS(3.0 * n/N)).
BlackmanHarris = 5
}
更多示例: Matlib——二维傅里叶变换
评论：
发表评论：