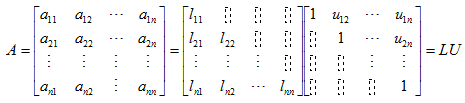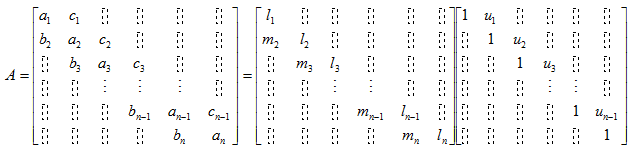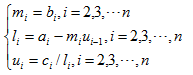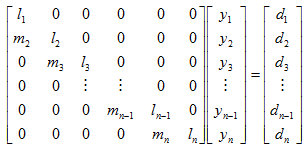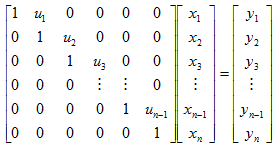任意矩阵A都可以通过克洛脱(Crout)分解得到两个三角矩阵：

如果A是三对角矩阵(非0元素排列在三条对角线上)，则克洛脱分解的结果为：

在分解后的矩阵中，,，其余各项的计算规则如下：

在得到了各个系数后，原方程组就可以分解为两个方程组，即：

对于第一个方程，求解向量y_i

其中y₁=d₁/l₁，其余各项的递推计算关系是：
(i=2，3，...，n)

对于第二个方程，求解最终结果x_i

其中x_n=y_n，其余各项的递推求解关系是：
(i=n-1，n-2，...，1)

       递推计算y_i和x_i的过程分别被形象地形容为“追的过程”和“赶的过程”，这也是追赶法(国际上叫作托马斯法)得名的原因。对三角矩阵的克洛脱分解需要满足几个条件，否则无法进行，这几个条件分别是：

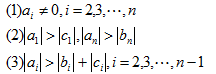
再附上一张网上找的LU分解图,感谢作者提供这么漂亮的图片
原图来自百度百科 https://baike.baidu.com/item/lu%E5%88%86%E8%A7%A3/764245?fr=aladdin

克洛脱(Crout)LU分解——C#实现