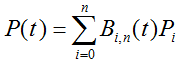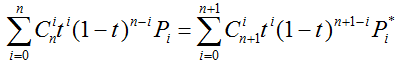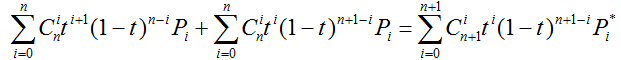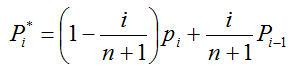所谓升阶是指保持Bézier曲线的形状与方向不变，增加定义它的控制顶点数，即提高该Bézier曲线的次数。增加了控制顶点数，仅能增加对曲线进行形状控制的灵活性，还在构造曲面方面有着重要的应用。对应一些由曲线生成曲面的算法，要求那些曲线必须是同次的。应用升阶的方法，可以把低于最高次数的曲线提升到最高次数，从而获得相同的次数。曲线升阶后，原控制顶点会发生变化。

设给定原始控制顶点P0，P1，...，Pn，定义了一条n次Bézier曲线

(0<=t<=1)

增加一个顶点，曲线提升一阶后，仍定义同一条曲线的新控制顶点为，则有

对上式左边乘以(t+(1-t))，得

比较等式两边项的系数，得

(这里把i代换成i-1)

两边除以，得

式中，

此式说明：

1) 新的控制顶点是以参数值i/(n+1)按分段线性插值从原始控制多边形得出的。

2) 升阶后新的控制多边形在原始控制多边形的凸包内。

3) 控制多边形更靠近曲线。

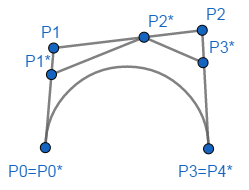
三次Bézier曲线的升阶实例如图所示。

       对于Bézier曲线的升阶可以无止境地进行下去，从而得到一个控制多边形序列，它们都定义同一条Bézier曲线。这个多边形序列将收敛到一个极限，就是所定义的该Bézier曲线。

       升阶的逆过程是降阶：即将一条n次Bézier曲线表示成n-1次。在大多数情况下，准确的降阶是不可能的。例如，具有拐点的三次Bézier曲线就不可能表示成二次。