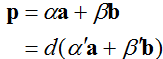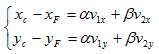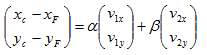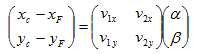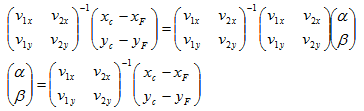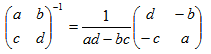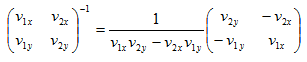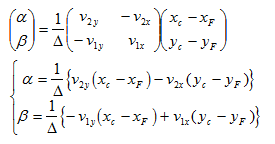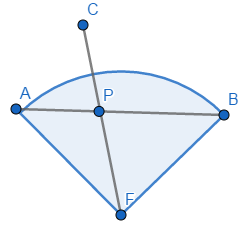
设向量v1=FA，向量v2=FB，向量p=FP，向量c=FC

向量的定比分公式:

用α表示(1-t)，β表示t，定比分公式可转换为:

(α≥0且β≥0且α+β=1)

当α与β满足上面的条件时，向量p就是向量a与向量b的内分点。当α+β不等于1，而是等于常数d时，等式可变形为:

其中α‘+β’=1，向量α‘a+β’b表示向量a与向量b的内分点。此时原向量p就等于这个内分点乘以常数d，那么如果在d>0的范围内移动d，向量p就会变成一个从扇形的圆心坐标开始、通过内分点的射线上的点(如上图的FC射线)。

对α与β进行各种取值(在正数范围内)，这条射线能通过的所有范围正是向量a与向量b之间的区域。

上式可以表示为:

(方程组)

(列向量表示)

(矩阵表示)

对上面的矩阵表示两边同时乘以个逆矩阵:

这里补充下2×2矩阵的逆矩阵计算公式:

根据逆矩阵公式可得:

这里将系数的分母表示为△，则有:

根据上面的公式计算出α与β的值，若α≥0且β≥0且FC≤FA，则点C在扇形内。(FA指扇形的半径)

       检测一点是否在两向量之间，也可以利用向量的外积进行检测，并且算式可能会更加简单，但一般来说，通过方程组求解的检测方式，可以适用于更多的情况。参见 矢量的叉积