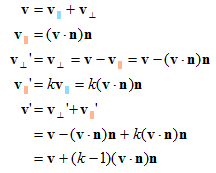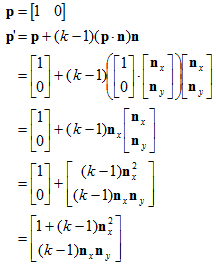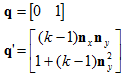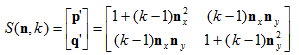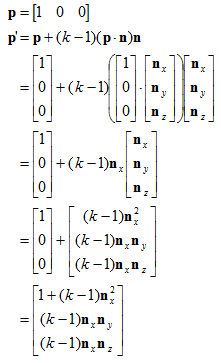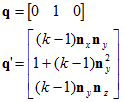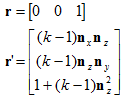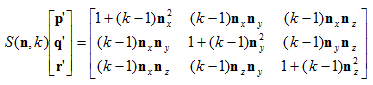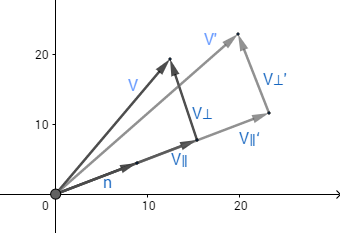
我们可以不依赖坐标系而沿任意方向进行缩放。设n为平行于缩放方向的单位向量，k为缩放因子，缩放沿穿过原点并平行于n的直线(2D中)或平面(3D中)进行。

      我们需要推导出一个表达式，给定向量v，可以通过v，n和k来计算v'。为了做到这一点，将v分解为两个分量，v∥和v⊥，分别平行于n和垂直于n，并满足v=v∥+v⊥。v∥是v在n上的投影，由(v●n)n可以得到v∥。因为v⊥垂直于n，它不会被缩放操作影响。因此，v'=v∥'+v⊥，剩下的问题就是怎样得到v∥'。由于v∥平行于缩放方向，v∥'可由公式kv∥得出。如图所示：

既然已经知道了怎样对任意向量进行缩放，当然也就可以据此计算缩放后的基向量。这里列出2D中的一个基向量的求法，基余的基向量依此类推。(注意下面采取列向量形式只是为了使等式形式好看一些)

通过基向量构造矩阵，得到以单位向量n为缩放方向，k为因子的缩放矩阵，如图

3D中基向量为：

以单位向量n为缩放方向，k为因子的3D缩放矩阵公式为：