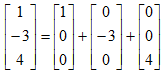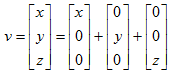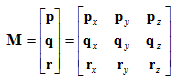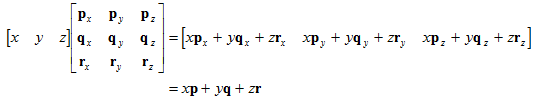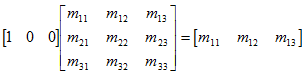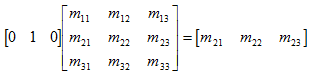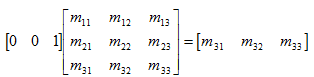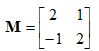一般来说，方阵能描述任意线性变换。线性变换保留了直线和平行线，而原点没有移动。线性变换保留直线的同时，其他的几何性质如长度、角度、面积和体积可能就被变换改变了。从非技术意义上说，线性变换可能“拉伸”坐标系，但不会“弯曲”或“卷折”坐标系。下面是一组非常有用的变换：

• 旋转
• 缩放
• 投影
• 镜像
• 仿射

矩阵是怎样变换向量的

向量在几何上能被解释成一系列与轴平行的位移。如，向量[1, -3, -4]能被解释成位移[1, 0, 0]，随后位移[0, -3, 0]，最后位移[0, 0, 4]。依据三角形法则将这个位移序列解释成向量的加法：

一般来说，任意向量v都能写为“扩展”形式：

注意右边的单位向量就是x，y，z轴。向量的每个坐标都表明了平行于相应坐标轴的有向位移。

让我们将上面的向量和重新写一遍，这次，分别将p，g和r定义为指向+x，+y和+z方向的单位向量:

将向量表示为基向量的线性组和

现在，向量v就被表示成向量p，q，r的线性变换了。向量p，q，r称作基向量。这里基向量是笛卡尔坐标轴，但事实上，一个坐标系能用任意3个基向量定义，当然这三个向量要线性无关(也就是不在同一平面上)。以p，q，r为行构建一个3×3矩阵M，可得到公式：

将矩阵解释为基向量集合

用一个向量乘以该矩阵，得到：

这和前面计算转换后的v的等式相同。我们发现关键点是：

如果把矩阵的行解释为坐标系的基向量，那么乘以该矩阵就相当于执行了一次坐标转换。若有aM=b，我们就可以说，M将a转换到b。

     从这一点看，术语“转换”和“乘法”是等价的。

     坦率地说，矩阵并不神秘，它只是用一种紧凑的方式来表达坐标转换所需的数学运算。进一步，用线性代数操作矩阵，是一种进行简单转换或导出更复杂转换的简便方法。

矩阵的形式

先看一下基向量[1, 0, 0], [0, 1, 0], [0, 0, 1]乘以任意矩阵M时的情况：

正如您所见，用基向量[1, 0, 0]乘以M时，结果是M的第1行。其他两行也有同样的结果。这是一个关键的发现：

矩阵的每一行都解释为转换后的基向量。

这个强有力的概念有两条重要性质：

• 有了一种简单的方法来形象化解释矩阵所代表的变换。
• 有了反向建立矩阵的可能——给出一个期望的变换(如旋转、缩放等)，能够构造一个矩阵代表此变换。我们所要做的一切就是计算基向量的变换，然后将变换后的基向量填入矩阵。这个技巧得到方泛应用。

看个2D实例:

从矩阵中抽出基向量p和q

x基向量变换至上面的p向量，y基向量变换至q向量。

3D中同理。

总结：

• 方阵的行能被解释为坐标系的基向量。
• 为了将向量从原坐标系变换到新坐标系，用它乘以一个矩阵。
• 从原坐标系到这些基向量定义的新坐标系的变换是一种线性变换。线性变换保持直线和平行线，但角度、长度、面积或体积可能会被改变。
• 零向量乘以任何矩阵仍然得到零向量。因此，方阵所代表的线性变换的原点和原坐标系的原点一致。变换不包含原点。
• 可以通过想象变换后的坐标系的基向量来想象矩阵。这些基向量在2D中构成“L”型，在3D中构成“三角架”型。用一个盒子及辅助物更有助于理解。