红黑树是一种自平衡搜索树。通过对节点进行着色和旋转，红黑树很容易保持树的平衡。

我们需要在二叉搜索树上增加一个额外的颜色信息，树中的节点可以涂成红色或黑色。如果一棵二叉搜索树满足下面的全部5条性质，则称为红黑树：

(1) 任一节点要么是红色，要么是黑色；
(2) 根节点为黑色；
(3) 所有叶节点(NIL节点)为黑色;
(4) 如果一个节点为红色，则它的两个子节点都是黑色；
(5) 对任一节点，从它出发到所有叶子节点的路径上包含相同数量的黑色节点。

为什么这5条性质能保证红黑树的平衡呢？因为它们有一个关键的特性：从根节点出发到达叶节点的所有路径中，最长路径不会超过最短路径的两倍。

注意第(4)条性质，它意味着不存在两个连续的红色节点。因此，最短的路径只含有黑色节点，任何比最短路径长的路径上都分散有一些红色节点。根据性质(5)，从根节点出发的所有路径都含有相同数量的黑色节点，这就最终保证了没有任何路径超过最短路径长度的两倍。

红黑树沿用所有二叉搜索树中不改变树结构的操作，包括查找、获取最大值、最小值等；只有插入和删除操作是特殊的。

示例: C#

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace RedBlackTree1
{
    class Program
    {
        static void Main(string[] args)
        {
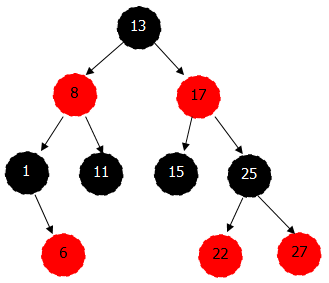
            int[] keys = new int[] { 13, 8, 1, 11, 6, 17, 15, 25, 22, 27};
            Console.Write("测试数据为: ");
            for (int i = 0; i < keys.Length; i++)
            {
                Console.Write(keys[i] + " ");
            }
            Console.WriteLine();

            //根节点
            Node root = null;
            //录入10个节点
            for (int i = 0; i < keys.Length; i++)
            {
                Node node = new Node();
                node.key = keys[i];
                if (null == root)
                    root = node;
                else
                    Insert(root, node);
            }
            Console.Write("构建的二叉搜索树为: ");
            Print(root);

            Console.WriteLine();
            Console.WriteLine("给二叉搜索树染色: ");
            Coloring(root, Color.Black);//根节点为黑色
            Print(root, true);

            Console.ReadKey();
        }

        static void Insert(Node root, Node child)
        {
            if(root.key >= child.key)
            {
                if (null == root.left)
                    root.left = child;
                else
                    Insert(root.left, child);
            }
            else
            {
                if (null == root.right)
                    root.right = child;
                else
                    Insert(root.right, child);
            }
        }

        static void Coloring(Node root, Color color)
        {
            if (null == root)
                return;
            root.color = color;
            color = (color == Color.Black) ? Color.Red : Color.Black;
            Coloring(root.left, color);
            Coloring(root.right, color);
        }

        static void Print(Node root, bool outputColor = false)
        {
            if (null != root.left)
                Print(root.left, outputColor);

            if (outputColor)
                Console.Write("{0}({1}) ", root.key, root.color);
            else
                Console.Write("{0}  ", root.key);

            if (null != root.right)
                Print(root.right, outputColor);
        }
    }

    public enum Color
    {
        Black,
        Red
    }

    public class Node
    {
        public Color color;
        public int key;
        public Node parent;
        public Node left;
        public Node right;
    }


}

运行测试

染色后对应的树状图为 (通常插图都省略了NIL节点)