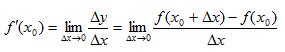一元非线性方程的求解是高等数学研究的重要课题之一，早在2000多年前，古巴比伦的数学家就能解一元二次方程了，中国的《九章算术》也有对一元二次方程求解的记载。目前人们普遍认为低阶(5阶以下)一元非线性方程可以通过求根公式求解，但是高于或等于5阶的一元非线性方程不存在求根公式，要精确求解非常困难。对高阶方程，一般采用迭代法近似求解，牛顿迭代法因为方法简单，迭代收敛速度快而被广泛使用。

     牛顿迭代法(Newton's method)又称牛顿——拉弗森方法(Newton-Raphson method)，它是一种在实数域和复数域上近似求解方程的方法。方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x)=0的根。

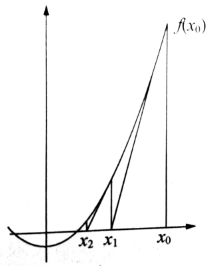
牛顿迭代法逼近示意图：

     首先，选择一个接近函数f(x)零点的x0作为迭代初始值，计算相应的f(x0)和切线斜率f'(x0)(这里f'(x)是函数f(x)的一阶导函数)。然后我们经过点(x0, f(x0))做一条斜率为f'(x0)的直线，该直线与x轴有一个交点，可通过以下方程的求解得到这个交点的x坐标：

求解这个方程，可以得到：

      我们将新求得的点的x坐标命名为x1，通常x1会比x0更接近方程f(x)=0的解。因此我们现在可以利用x1开始下一轮迭代。根据上述方程中x1和x0的关系，可以得到一个求解x的迭代公式：

      这就是牛顿迭代公式。目前已经证明，如果f(x)的一阶导函数f'(x)是连续函数，并且待求的零点x是孤立的，则在零点x周围存在一个区间，只要初始值x0位于这个区间，牛顿迭代必定收敛。并且，只要f'(x)≠0，牛顿迭代法具有平方收敛的性能。这意味着每迭代一次，结果的有效数字将增加一倍，这比二分逼近法的线性收敛速度快了一个数量级。

导函数的求解与近似公式

示例

using System;

namespace NewtonTest
{
    class Program
    {
        public delegate double Function(double x);
        const double PRECISION = 0.1;//计算精度

        static void Main(string[] args)
        {
            double x = NewtonRaphson(TestFun, -8);
            Console.WriteLine("f({0})={1}", x, TestFun(x));
            Console.Read();

        }

        //示例方程：一元二次方程
        //求解y=0时,x的值.
        public static double TestFun(double x)
        {
            //注意：要确保这个方程是有解的。
            double y = 5 * Math.Pow(x, 2) + 8 * x + 2;
            return y;
        }

        /// <summary>
        /// 计算函数f在x附近的一阶导数值
        /// </summary>
        /// <param name="f">原函数</param>
        /// <param name="x">x值</param>
        /// <returns></returns>
        public static double CalcDerivative(Function f, double x)
        {
            return (f(x + 0.000005) - f(x - 0.000005))/0.00001;
        }

        /// <summary>
        /// 牛顿迭代法
        /// 用于求解一元非线性方程
        /// </summary>
        /// <param name="f">原函数</param>
        /// <param name="x0">迭代初始值</param>
        /// <returns></returns>
        public static double NewtonRaphson(Function f, double x0)
        {
            double x1 = x0 - f(x0) / CalcDerivative(f, x0);
            while(Math.Abs(x1 - x0) > PRECISION)
            {
                x0 = x1;
                x1 = x0 - f(x0) / CalcDerivative(f, x0);
            }
            return x1;
        }
    }
}

运行结果