1. 从几何意义出发

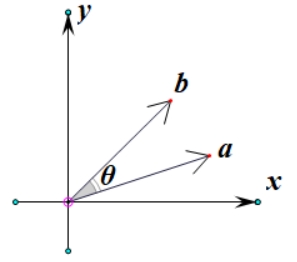
  二维叉积的几何意义是两个向量张成的平行四边形的有向面积。其绝对值等于平行四边形的面积，符号由两个向量的相对方向决定（右手法则）。

平行四边形的面积公式为： $$ S=|a|\cdot|b|\cdot\sin\theta $$ 其中 $\theta$ 是 a 和 b 之间的夹角。

2. 用坐标表示：

• 设 $a=(a_x,a_y), \quad b=(b_x,b_y)$
• 利用三角恒等式： $\sin(\beta-\alpha)=\sin\beta\cos\alpha-cos\beta\sin\alpha$
  其中 $\alpha$ 是 a 与 x 轴的夹角，$\beta$ 是 b 与 x 轴的夹角。
• 因为：
  $ \begin{aligned} &\cos\alpha=\frac{a_x}{|a|},\quad \sin\alpha=\frac{a_y}{|a|} \\ &\cos\beta=\frac{b_x}{|b|},\quad \sin\beta=\frac{b_y}{|b|} \end{aligned} $
• 代入面积公式：
  $ \begin{aligned} S&=|a|\cdot|b|\cdot \left(\frac{b_y}{|b|} \frac{a_x}{|a|} - \frac{b_x}{|b|}\frac{a_y}{|a|} \right) \\ &=a_xb_y-a_yb_x \end{aligned} $
• 因此，二维叉积的坐标公式为：
  $ a \times b = a_xb_y-a_yb_x $

注意：平行四边形的面积=向量叉积=矩阵行列式