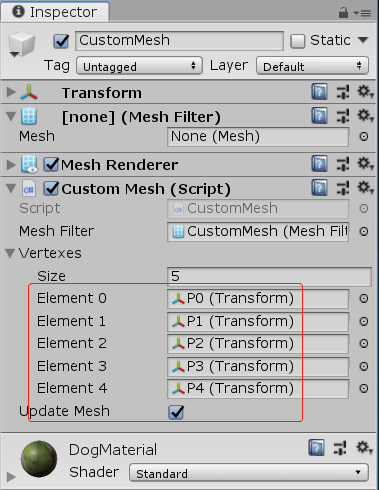
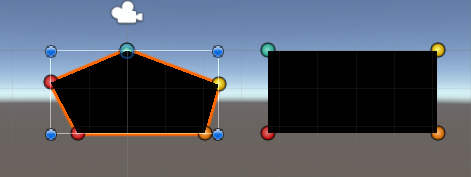
示例：通过编辑顶点自定义Mesh形状

CustomMesh.cs

using System.Collections;
using System.Collections.Generic;
using UnityEngine;
/// <summary>
/// 自定义Mesh
/// </summary>
public class CustomMesh : MonoBehaviour
{
    public MeshFilter meshFilter;
    public Transform[] vertexes;

    private List<Vector3> vertices;//Mesh顶点
    private List<int> triangles; //Mesh三角形
    private Mesh mesh = null;
    private List<Vector3> points;
    //映射: 顶点->顶点序号
    private Dictionary<Vector3, int> indexDic = new Dictionary<Vector3, int>();

    public bool updateMesh = true;

    private void Update()
    {
        if (!updateMesh)
            return;

        updateMesh = false;
        GenerateMesh();
    }

    private void GenerateMesh()
    {
        if (vertexes.Length <= 3)
            return;

        if (vertices == null)
            vertices = new List<Vector3>();
        vertices.Clear();

        if (triangles == null)
            triangles = new List<int>();
        triangles.Clear();

        if (points == null)
            points = new List<Vector3>();
        points.Clear();

        Bounds bounds = new Bounds();
        int i = 0;
        int n = vertexes.Length; //多边形顶点数
        for (i = 0; i < n; i++)
        {
            Vector3 localPosition = vertexes[i].localPosition;
            points.Add(localPosition);
            vertices.Add(localPosition);
            indexDic[localPosition] = i;
            bounds.Encapsulate(localPosition);
        }

        //对简单多边形进行三角剖分
        i = 0;
        Vector3 Q0 = points[i];
        Vector3 Q1, Q2;
        while(n > 3)
        {
            Q1 = points[i + 1];
            Q2 = points[i + 2];
            Debug.LogFormat("Test({0}, {1}, {2})", indexDic[Q0], indexDic[Q1], indexDic[Q2]);
            if (Test(Q0, Q1, Q2))
            {
                //输出三角形Q0Q1Q2
                triangles.Add(indexDic[Q0]);
                triangles.Add(indexDic[Q1]);
                triangles.Add(indexDic[Q2]);
                Debug.LogFormat("输出三角形{0},{1},{2}", indexDic[Q0], indexDic[Q1], indexDic[Q2]);
                //删除顶点Q1
                DeletePoint(Q1);
                n--;
            }
            else
            {
                Q0 = Q1;
                i++;
            }
            
            if (i + 2 >= points.Count)
                break;
        }
        //输出最后剩下的一个三角形
        triangles.Add(indexDic[points[0]]);
        triangles.Add(indexDic[points[1]]);
        triangles.Add(indexDic[points[2]]);
        Debug.LogFormat("输出三角形{0},{1},{2}", indexDic[points[0]], indexDic[points[1]], indexDic[points[2]]);

        //创建Mesh
        if (mesh == null)
            mesh = new Mesh();

        List<Vector2> uv = new List<Vector2>();
        for (i = 0; i < vertices.Count; i++)
        {
            float u = (vertices[i].x - bounds.min.x) / bounds.size.x;
            float v = (vertices[i].y - bounds.min.y) / bounds.size.y;
            uv.Add(new Vector2(u, v));
        }
        mesh.vertices = vertices.ToArray();
        mesh.triangles = triangles.ToArray();
        mesh.uv = uv.ToArray();

        if (meshFilter != null)
            meshFilter.sharedMesh = mesh;
    }

    private void DeletePoint(Vector3 P)
    {
        for (int i = 0; i < points.Count; i++)
        {
            Vector3 p = points[i];
            if (p == P)
            {
                points.RemoveAt(i);
                break;
            }
        }
    }

    /// <summary>
    /// 检查Q0Q2是否为完全在原多边形内部的对角线(true: 是)
    /// </summary>
    /// <param name="Q0">三角形顶点</param>
    /// <param name="Q1">三角形顶点</param>
    /// <param name="Q2">三角形顶点</param>
    /// <returns></returns>
    private bool Test(Vector3 Q0, Vector3 Q1, Vector3 Q2)
    {
        Vector3 P = Q1 - Q0;
        Vector3 Q = Q2 - Q0;

        bool zEqual = (Q0.z == Q1.z && Q1.z == Q2.z);

        //这里规定顶点都按顺时针方向排列(即，向右转向)
        //判断向量转向,排除共线或凹角的情况
        if (zEqual && CrossProduct(P, Q) >= 0)
        {
            return false;//左转或共线
        }

        //是否存在多边形的其他顶点在三角形内部
        for (int i=0; i<points.Count; i++)
        {
            Vector3 p = points[i];
            if (p == Q0 || p == Q1 | p == Q2)
                continue;
            //考虑第三维度
            if (p.z != Q0.z || p.z != Q1.z || p.z != Q2.z)
                continue;
            if (IsPointInTriangle(p, Q0, Q1, Q2))
                return false;//存在多边形的其他顶点在三角形内部
        }
        return true;
    }

    /**
    * 点积(内积)
    * (P, Q)表示向量P和Q的夹角。
    * 
    * 如果P和Q不共线,则:
    * P·Q > 0，则P和Q的夹角是钝角(大于90度)
    * P·Q < 0，则P和Q的夹角是锐角(小于90度)
    * P·Q = 0，则P和Q的夹角是90度
    */
    private static float DotProduct(Vector3 P, Vector3 Q)
    {
        return P.x * Q.x + P.y * Q.y + P.z * Q.z;
    }

    // 判断P是否在三角形Q0Q1Q2内
    public static bool IsPointInTriangle(Vector3 P, Vector3 P0, Vector3 P1, Vector3 P2)
    {
        float s012 = CalculateTriangleArea(P0, P1, P2);
        double s01p = CalculateTriangleArea(P0, P1, P);
        double s02p = CalculateTriangleArea(P0, P2, P);
        double s12p = CalculateTriangleArea(P1, P2, P);
        return s01p + s02p + s12p <= s012;
    }

    // 计算三角形面积
    public static float CalculateTriangleArea(Vector3 P0, Vector3 P1, Vector3 P2)
    {
        float s = CrossProduct(P0 - P1, P2 - P1) / 2;
        return s;
    }

    /**
    * 叉积(外积)
    * P×Q = -(Q×P)
    * 
    * 几何意义:
    * P×Q为所构成的平行四边行的面积。
    * 
    * 方向:
    * P×Q的方向是垂直于P和Q所在的平面(右手坐标系)
    * 
    * 性质:
    * 判断两矢量相互之间的位置关系
    * P×Q > 0，则Q在P的逆时针方向
    * P×Q < 0，则Q在P的顺时针方向
    * P×Q = 0，则Q与P共线
    */
    private static float CrossProduct(Vector3 P, Vector3 Q)
    {
        return (P.y*Q.z - Q.y*P.z) + (P.z*Q.x - Q.z*P.x) + (P.x*Q.y - Q.x*P.y);
    }
}