在一个无向连通图G中，如果取它的全部顶点和一部分边构成一个子图G`，即V(G`)=V(G)和E(G`)⊆E(G`)。若边集E(G`)中的边，即将图G中的所有顶点连通，又不形成回路，则称子图G`是原图G的一棵生成树。显然无向连通图的生成树不是唯一的。连通图的一次遍历所经过的边的集合及图中所有顶点的集合就构成了该图的一棵生成树，对连通图的不同遍历，就得到了不同的生成树。

       对于一个带权图，具有权值之和最小的生成树称为图的最小生成树。最小生成树的概念可以应用到许多实际问题中，例如，以尽可能低的总造价建造若干条高速公路，把n个城市联系在一起等都涉及最小生成树的概念。

       产生一个图的最小生成树主要有两个算法，即普里姆算法和克鲁斯卡尔算法。

示例：C++

#include "pch.h"
#include <iostream>

typedef struct
{
	int u; //边的起始顶点
	int v; //边的终止顶点
	int w; //边的权值
} Edge;

#define MAXVEX 10

void PrintVset(int vset[], int n)
{
	for (int i = 0; i < n; i++)
		printf("%d, ", vset[i]);
	printf("\n");
}

//克鲁斯卡尔算法；适合稀疏图。
void Kruskal(Edge E[], int n, int e)
{
	int i, j, m1, m2, sn1, sn2, k;
	int vset[MAXVEX];
	//初始化辅助数组
	for (i = 0; i < n; i++) vset[i] = i;
	k = 1; //构造最小生成树的第几条边
	j = 0; //E中边的下标
	//生成的边数小于n时循环
	while (k < n)
	{
		//取一条边的头尾顶点
		m1 = E[j].u; m2 = E[j].v;
		//分别得到两个顶点所属的集合编号
		sn1 = vset[m1]; sn2 = vset[m2];
		if (sn1 != sn2)
		{
			printf("  边(%d,%d)权为:%d\n", m1, m2, E[j].w);
			k++;
			//两个集合统一编号
			//将图中同一棵子树上的顶点标成统一编号，
			//当一个顶点连接到树中时，将此顶点编号改成树中顶点编号。
			//当图中一棵子树连到另一棵子树时，将此子树顶点编号统一改成另一棵子树的编号。
			//从而避免已经在同一棵树中的两个顶点再次相连(因为属于同一棵树的顶点编号是相同的)。
			//下面的循环保证了属于同一棵树的顶点编号是相同的。
			for (i = 0; i < n; i++) {
				if (vset[i] == sn2) {
					vset[i] = sn1;
					printf("[%d]: %d->%d: ", i, sn2, sn1);
					PrintVset(vset, 7);
				}
			}
		}
		j++; //扫描下一条边
	}
}

int main()
{
	std::cout << "克鲁斯卡尔算法\n";

	int n = 7, e = 10;
	Edge E[] = {
		{3,5,30},{1,4,40},{3,6,42},
		{2,6,45},{0,1,50},{3,4,50},
		{2,3,52},{0,2,60},{1,3,65},
		{4,5,70}
	};
	printf("最小生成树:\n");
	Kruskal(E, n, e);
	return 0;
}

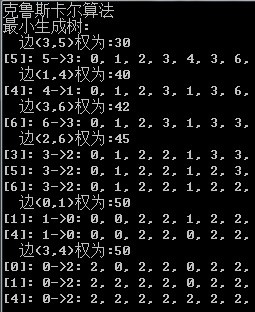
运行测试